Квантовая теория теплоемкости идеального газа
Классическая теория столкнулась как вы понимаете с непреодолимыми трудностями при построении теории теплоемкости 2х атомного газа(сколько степеней свободы и когда учитьывать) через равно распред энерг по степ своб и теорему о вирриале) рассмотрим теперь вопрос о теплоемкости ид газов с пом. Кв стат. по скольку молек. Газа тождественны, стат сумма может быть записана в виде
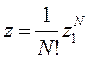 (25) где
(25) где 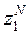 -ст. сумма для одной частицы
-ст. сумма для одной частицы
теперь Z1 ; 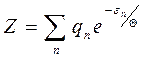 суммирование по всем возможным кв уровням одной молекулы ε=εпоступ +εвнут, и Z1=ZпоступZвнут
суммирование по всем возможным кв уровням одной молекулы ε=εпоступ +εвнут, и Z1=ZпоступZвнут
поступательное дв-е молекул в ид газе можно рассматривать как в классике, т.к. среднее расстояние м-ду частицами >> длинны волны Де-Броиля Zпоступ (часть стат суммы связанная с поступ движением) двухат молекулы, ни чем не отлич от стат суммы одноатомн молек, по скольку она дв-ся в пространстве как мат. Точка с массой m=m1+m2 Поэтому и теплоемкость связана с поступ дв-ем такая же как в классике
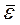 =U=3/2kT Cv=3/2Nk|N=N* Cv=3/2R
=U=3/2kT Cv=3/2Nk|N=N* Cv=3/2R
Что с внутренней энергией? Внут энерг связ с колеб, вращ дв-я и электронной энергией. Последняя не существенна и можно не рассматривать.
εвнут=εvib +εrot (u= uvib +urot)
Воспользуемся (7)
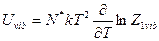 (26)
(26)
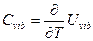
Из (11): 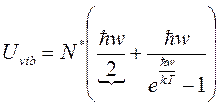
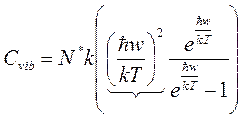 (27)
(27)
введем характ. Темп.
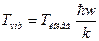 , то (27) для 1 моля
, то (27) для 1 моля
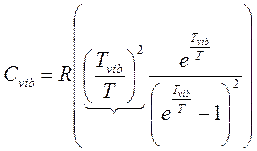
при T<<Tvib Cvib→0?
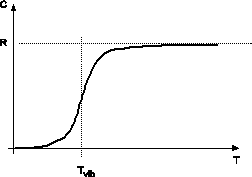
(ТЕПЛ ехр убывает при при T>>Tvib exp→1,и числ/знаменат=1
)
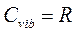 -клас. Знач.(равн. Распр. +т. О вириале)
-клас. Знач.(равн. Распр. +т. О вириале)
при низких температурах степени своб вымерз
Аналог ситуация для вращ степени своб(т.к. квантовый ротатор)для него
εrj=ћ2/I(j(j+1)) (28)
I- момент инерц молек, j=0 1 2 …
Кажд сост (2j+1), крайно. вырождно
qj=2j+1
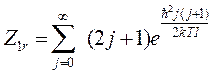 (29)
(29)
Tr(вводим)=ћ2/2кI характ температуры
Можно показать при T>>Tr Cr≈R
приT<<Tr Cr~3(Tr/T)2Nkexp(-Tr/T)→0
картинка аналогична Для Н2
Tr=85,4 K
Tv=6100 K
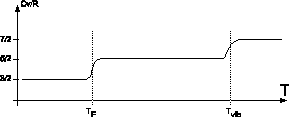
Дата добавления: 2021-05-28; просмотров: 597;











