Понятие о явлениях переноса

Взаимодействие молекул, в частности столкновение между молекулами газа, играет важную роль в процессе установления равновесного состояния.

Практически в земных условиях из-за наличия сил сопротивления (сил трения) все системы, в которых не происходит притока энергии извне, являются диссипативными. Если диссипативную систему вывести из состояния равновесия, а затем предоставить самой себе, то она постепенно перейдёт в равновесное состояние. Время, в течение которого система достигает равновесного состояния, называют временем релаксации. Время релаксации различно относительно разных параметров, по которым система может отклоняться от равновесного состояния.

Взаимодействия молекул, их столкновения, являются тем механизмом, который приводит систему (газ) в равновесное состояние. В идеальном газе столкновения происходят в основном между парами молекул, одновременным столкновением трёх и более молекул можно пренебречь.

Вывести систему, представляющую собой идеальный газ, из равновесного состояния можно, например, нагрев одну часть газа, то есть нарушить тепловое равновесие. Если газ после этого предоставить самому себе, то через некоторое время температура снова станет одинаковой во всех частях газа. Это выравнивание происходит благодаря непрерывному тепловому движению молекул. В нагретой части больше быстрых молекул, имеющих большую тепловую энергию, чем в других частях газа, поэтому быстрые молекулы переходят туда, где их меньше, таким образом, их число становится равным повсюду.

Одновременно происходит перемещение молекул и в нагретую область, благодаря соударениям, так что число частиц в единице объёма в среднем не изменяется. Происходит только перенос энергии из той части газа, где она больше, туда, где она меньше. Этот процесс называется теплопроводностью.

Если систему вывести из равновесия, добавив примесь другого газа, так, чтобы при одинаковых во всём объёме давлении и температуре, концентрация примеси в одной части была выше, чем во всех других, то спустя определённое время система перейдёт в равновесное состояние за счёт перемещения молекул примеси из области с большей концентрацией в область с меньшей концентрацией. В данном процессе, который называется диффузией, происходит перенос массы примеси. Время релаксации системы в этом случае не равно времени релаксации системы, стремящейся к тепловому равновесию.

Равновесие газа может быть нарушено, если одной из его частей сообщена скорость, отличная от скорости течения соседних частей. В этом случае через некоторое время, благодаря переносу импульса упорядоченного движения от более быстрых слоёв к менее быстрым, скорости слоёв выравниваются. Этот процесс называется вязкостью.

Все эти процессы можно рассматривать как явления переноса, подходя к их изучению с формальной стороны одинаково: выделяя переносимую величину, выделяя причину переноса, вводя уравнение переноса и времена релаксации.

Как уже было отмечено выше, механизм, который приводит систему (газ) в равновесное состояние, обусловлен столкновениями молекул. Основные характеристики молекулярного движения были рассмотрены нами в п. 11.4.

Диффузия в газах

Диффузией называется явление взаимного проникновения двух или нескольких соприкасающихся веществ. Каждый из компонентов смеси переходит из области с большей концентрации в область с меньшей концентрацией. При диффузии, таким образом, происходит перенос вещества. Диффузия в газах возникает и в том случае, если они неоднородны по концентрации или плотности (самодиффузия). Для количественного описания этого явления используют понятие диффузионного потока. Диффузионный поток можно выразить через массу переносимого вещества или через число молекул (или молей) переносимого вещества.

Диффузионный поток как поток массы определяется массой вещества, перенесённого через площадку dS, перпендикулярную направлению переноса, в единицу времени. Часто используют понятие плотности диффузионного потока. Плотность диффузионного потока определяется массой вещества, перенесённого через единичную площадку, перпендикулярную направлению переноса, в единицу времени. Плотность диффузионного потока равна:

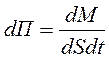, (14.1)

где dM- элемент массы вещества, переносимого через бесконечно малую площадку dS , перпендикулярную направлению переноса, за бесконечно малый промежуток времени dt.

Диффузионный поток как поток частиц определяется числом частиц вещества, перенесённого через площадку dS, перпендикулярную направлению переноса, в единицу времени. Плотность диффузионного потока определяется числом частиц вещества, перенесённого через единичную площадку, перпендикулярную направлению переноса, в единицу времени. В этом случае плотность диффузионного потока равна:

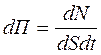, (14.2)

где dN- элементарное число частиц вещества, переносимого через бесконечно малую площадку dS , перпендикулярную направлению переноса, за бесконечно малый промежуток времени dt.

Основной закон диффузии – закон Фика: плотность диффузионного потока какого-либо компонента вещества прямо пропорциональна градиенту концентрации (плотности) этого компонента со знаком «минус»:

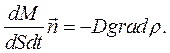(14.3)

Здесь 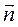- вектор положительной нормали к площадке, через которую переносится вещество; его направление совпадает с направлением переноса вещества. Градиент плотности grad p - это вектор, который, характеризует быстроту изменения скалярной величины – плотности - в пространстве и направлен в сторону наиболее быстрого возрастания данной плотности. D - коэффициент диффузии. Знак «минус» показывает, что направление потока вещества противоположно градиенту плотности.

Градиент плотности можно записать так:

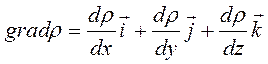, (14.4)

где 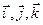- единичные вектора, направленные вдоль осей x,y,z, соответственно.

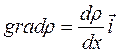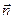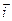Для одномерного случая и уравнение (14.3) может быть переписано в скалярном виде при условии, что направления векторов и совпадают:

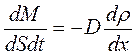(14.5)

Аналогично можно записать закон Фика и через поток частиц:

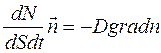(14.6)

Коэффициент диффузии численно равен плотности диффузионного потока при единичном градиенте концентрации (плотности) и СИ измеряется в 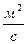. В системе СГС используют единицу измерения 1 Стокс = .

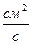В идеальных газах механизм переноса вещества обусловлен соударениями молекул, поэтому, чем выше температура газа, тем больше диффузионный поток и коэффициент диффузии. Коэффициент диффузии, а точнее самодиффузии (диффузии вещества самого в себя, обусловленной неоднородностью концентрации) для идеальных газов можно выразить так:

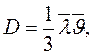(14.7)

где 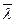- средняя длина свободного пробега молекул идеального газа, 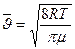- средняя арифметическая скорость молекул. При фиксированной температуре 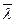обратно пропорциональна давлению, а скорость является постоянной, поэтому коэффициент диффузии. обратно пропорционален давлению. При фиксированном давлении 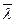прямо пропорциональна Т, а средняя арифметическая скорость ~ 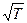, поэтому коэффициент диффузии в этом случае пропорционален .

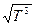Диффузия бывает нестационарной и стационарной. При нестационарной диффузии с течением времени благодаря переносу вещества выравниваются концентрации первоначально неоднородных областей. Разность концентраций со временем убывает по экспоненциальному закону:

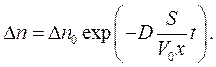(14.8)

Здесь 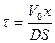- время релаксации, то есть время, в течение которого концентрация диффузионного потока уменьшается в е раз; x – расстояние, на котором определяется разность концентраций; S – площадь, через которую происходит диффузия; 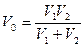- приведённый объём; V₁ – объём области с концентрацией n₁; V₂ – объём области с концентрацией n₂, определяющих разность концентраций

.

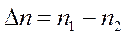Стационарная диффузия наблюдается при поддержании постоянным градиента концентрации, и, следовательно, диффузионного потока.

Вязкость газов

Вязкость газов – это свойство, благодаря которому выравниваются скорости упорядоченного движения разных слоёв газа. Можно дать и другое определение. Вязкость газов – это явление переноса, при котором происходит перенос импульса упорядоченного движения от слоёв, движущихся с большей скоростью, к слоям, движущимся с меньшей скоростью. Переносимый импульс можно количественно оценить с помощью потока импульса, равного импульсу упорядоченного движения слоёв, переносимому через площадку dS, параллельную слоям и перпендикулярную к направлению переноса, в единицу времени. Плотность элементарного потока импульса можно записать так:

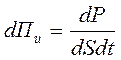(14.9)

Основной закон вязкости: плотность потока импульса прямо пропорциональна градиенту скорости со знаком «минус».

Знак «минус» показывает, что направление потока импульса противоположно направлению градиента скорости упорядоченного движения.

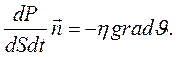(14.10)

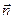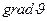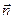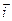Здесь - вектор положительной нормали к площадке S, через которую переносится импульс, его направление совпадает с направлением переноса импульса, - градиент скорости, направлен в сторону наиболее быстрого возрастания скорости, η- коэффициент динамической вязкости. Для одномерного случая, когда направления векторов и совпадают:

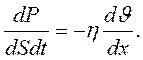(14.11)

Динамический коэффициент вязкости численно равен потоку импульса при единичном градиенте скорости. В СИ он измеряется в 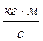или в Па^.с.

Для идеальных газов коэффициент динамической вязкости можно выразить следующим образом:

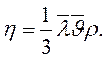(14.12)

Коэффициент вязкости зависит прямо пропорционально от 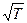и не зависит от давления, поскольку в формулу (5.23) входят как сомножители средняя длина свободного пробега, обратно пропорциональная давлению при фиксированной температуре, и плотность газа, прямо пропорциональная давлению.

Можно записать основной закон вязкости и через силу вязкого трения, которая направлена по касательной к слоям (к площадке S), используя второй закон Ньютона, согласно которому 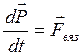. Для одномерного случая получим:

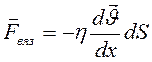(14.13)

Явление вязкости бывает стационарным и нестационарным. О стационарной вязкости говорят, когда градиент скорости поддерживают постоянным. Нестационарная вязкость происходит с изменением градиента, в результате выравниваются скорости взаимодействующих слоёв.

Для измерения коэффициента вязкости используют приборы – вискозиметры. Для измерения коэффициента вязкости необходимо, чтобы движение газа было ламинарным, то есть плавным, без завихрений. Этого можно достичь в очень узких трубках – капиллярах. Поэтому такие вискозиметры, в которых используют капилляры, называют капиллярными вискозиметрами.