Средняя длина свободного пробега молекул

Средняя скорость молекул газа весьма велика. Она составляет сотни и даже тысячи метров в секунду. Однако, совершая беспорядочное дви­жение, молекулы газа при нормальных условиях испытывают огромное число соударений в течение 1 с и расстоя­ния, проходимые ими от одной точки до другой, оказываются намного большими, чем перемещение L. Допустим, что молеку­ла движется от точки А к точке В (см. рисунок). Ее траектория вследствие соударений дан­ной молекулы с другими молекулами явля­ется ломаной линией. Проследить точно за траекторией частицы, пришедшей из точки А в точку В, невозможно, поэтому реальное смещение молекулы в газе оцени­вают скоростью диффузии:(отно­шением перемещения L молекулы из А в В к времени, за которое про­изошло это перемещение). Ско­рость диффузии молекулы значи­тельно меньше средней скорости ее молекулярного движения. Чтобы оценить скорости диффузии молекул, вводится понятие сред­ней длины свободного пробега . 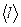Это такой путь, который молекула проходит, не испытывая соударений.

Допустим, что в единичном объеме содержится n₀ молекул, каждая из которых может быть представлена в виде шарика радиусом r. Будем считать, что траектория данной молекулы А прямолинейна (хотя в действительности это не так), а все молекулы, встречающиеся на ее пути, неподвижны. На своем пути молекула А несколько раз столкнется с дру­гими молекулами, центры которых лежат не дальше чем на 2r от траектории ее движения. Следовательно, можно предположить, что область, в которой происходит взаимодействие данной молекулы с дру­гими, — это цилиндр, радиус которого 2r.

За 1 с движущаяся молекула столкнется с теми молекулами, которые находятся внутри цилиндра, и пройдет путь, численно равный ее скоро­сти 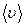.Объем цилиндра численно равен V=4πr² 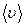n₀, а среднее число столкновений молекулы А с молекулами, находящимися в объеме цилин­дра, равно

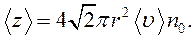(11.23)

Средняя длина свободного пробега молекулы равна отношению пу­ти, пройденного молекулой за одну секунду к числу происшедших за это время столкновений:

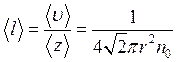(11.24)

Из выражения (11.24) следует, что (/) не зависит от температуры газа, так как с повышением температуры возрастают скорость и число столкновений.

При взаимодействии молекулы могут сближаться до некоторого наименьшего расстояния, называемого эффективным диаметром молекулы. Если d_эф = 2r, то из (11.24) имеем

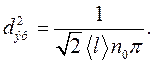(11.25)

Формулы (11.24) и (11.25) могут быть использованы для вычисления эффективного диаметра молекулы газов, длины свободного пробега и концентрации молекул.

Известно, что в одном моле вещества содержится 6,02 ^.10²³ моле­кул. Моль при нормальных условиях занимает объем V₀ = 22,4 10^{-3 м3} . Следовательно, в 1 м³ любого газа при нормальных условиях содержится одинаковое число молекул (N_л):

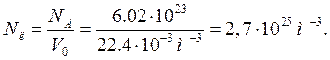(11.26)

Это число получило название постоянной Лошмидта.

Состояние газа, при котором средняя длина свободного пробега 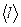молекул сравнима с размерами l сосуда, в котором заключен газ, называ­ют вакуумом.

Разреженное состояние газа, при котором средняя длина свободного пробега молекул становится больше линейных размеров сосуда, в котором находится газ, называется физическим вакуумом.

Понятие физического вакуума относительно. Чем больше линейные размеры сосуда с газом, тем при меньших давлениях в нём создаются условия вакуума. При нормальных атмосферных условиях 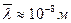, то есть, условия вакуума соблюдаются лишь в очень малых объёмах с линейными размерами порядка 10^{-8 м, а при давлениях 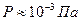, средняя длина свободного пробега 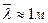, а значит, условия вакуума соблюдаются в достаточно больших объёмах.}