Лекция 12 Реальные газы, жидкости и твердые тела

12.1 Уравнение состояния реальных газов

12.2 Внутренняя энергия реального газа

12.3 Свойства жидкостей и твердых тел

12.4 Фазовые переходы первого и второго рода

12.1 Уравнение состояния реальных газов

При рассмотрении идеальных газов предполагалось, что молекулы подобны материальным точкам, собственный объем молекул не прини­мался во внимание, не учитывались силы межмолекулярного взаимодей­ствия. Такие предположения позволили построить молекулярно-кинетическую теорию, рассмотреть явления переноса и др.

Наличие межмолекулярных сил взаимодействия и конечные размеры молекул являются основными отличиями реальных газов от идеальных. Эти отличия непрерывно возрастают с увеличением давления.

Учет конечных размеров молекул и сил притяжения между ними по­зволяет получить уравнение состояния реальных газов из уравнений Кла­пейрона—Менделеева путем внесения поправки a/V² к давлению и по­правки b к объему:

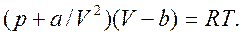(12.1)

Это уравнение называется уравнением Ван-дер-Ваальса. Записано оно для 1 моля газа. Поправка b, внесенная к объему, учитывает объем, занимаемый мо­лекулами реального газа, и мертвое пространство, т. е. объем зазоров между молекулами при их плотной упаковке. Поправка a/V² к давлению учитывает силы взаимодействия между молекулами реальных газов. Эта поправка представляет собой внутрен­нее давление, возникающее из-за взаимного притяжения между молеку­лами. Воздействие молекул друг на друга осуществляется в пределах ра­диуса молекулярного действия. Константы а и b могут быть оп­ределены для каждого газа опытным путем по критическим параметрам.

Учитывая большое значение уравнения Ван-дер-Ваальса, остано­вимся на его характеристике более подробно. Рассмотрим графическое изображение изотерм Ван-дер-Ва­альса на диаграмме р, V (рисунок 12.1).

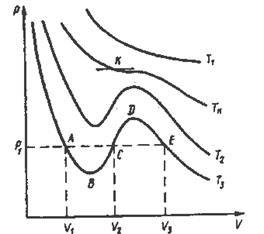
Рисунок 12.1 – Изотермы Ван-дер-Ва­альса

Как видно из диаграммы, вид изотерм зависит от температуры, при которой протекает изотермиче­ский процесс. На изотерме Т₃ < Т₂ < Т_к одному значению давления р соот­ветствуют три значения объема: V₁, V₂, V₃. Для изотермы Т_к характерно наличие точки перегиба К, изотерма Т₁ > Т_к имеет вид плавной кривой, совпадающей с изотермой для идеаль­ного газа.

Уравнение Ван-дер-Ваальса — уравнение третьей степени относи­тельно объема V, поэтому оно имеет или три вещественных корня (при Т < Т_к,) или один вещественный и два комплексно-сопряженных, не имеющих физического смысла (при Т > Т_к ) корня, т. е. при температуре ниже Т_к одному значению давления соответствуют три значения объема, при температуре выше Т_к одному значению давления соответствует одно значение объема. Отсюда следует, что при температуре выше Т_к вещество находится в однофазном газообразном состоянии, а при температуре ни­же Т_к вещество одновременно находится в двух фазовых состояниях.