I.1.9 ЯВЛЕНИЯ ПЕРЕНОСА В ГАЗАХ
В термодинамически неравновесных системах возникают необратимые процессы, такими, в частности будут явления переноса. Явления переноса объединяют группу процессов, связанных с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоёв вещества. Выравнивание неоднородностей приводит к возникновению явлений переноса. К явлениям переноса относятся диффузия, внутреннее трение и теплопроводность.
Явления переноса в газах и жидкостях состоят в том, что в этих веществах возникает упорядоченный, направленный перенос массы (диффузия), импульса (внутреннее трение) и внутренней энергии (теплопроводность). При этом в газах нарушается полная хаотичность движения молекул и максвелловское распределение молекул по скоростям.
Для простоты ограничимся одномерными явлениями переноса. Систему отсчёта будем выбирать так, чтобы ось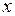 
была ориентирована в направлении переноса.
Теплопроводность. Если температура газа в разных местах различна, то и средняя энергия молекул также будет различной. Перемещаясь вследствие теплового движения из одних мест в другие, молекулы переносят запасённую ими энергию, что и обусловливает процесс теплопроводности.
Перенос энергии в форме теплоты подчиняется закону Фурье
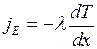, (I.42)
где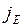 
– плотность теплового потока – величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х;
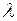– коэффициент теплопроводности (приложение Б., таблица Б.8);
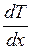– градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке.
Знак минус в уравнении (I.42) показывает, что теплота течёт в направлении убывания температуры, в связи, с чем знаки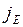 
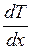и противоположны. Теплопроводность 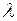численно равна плотности теплового потока при градиенте температуры, равном единице.
Коэффициент теплопроводности можно определить по формуле
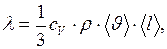(I.43)
где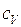 
– удельная теплоёмкость газа при постоянном объёме;
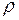– плотность газа; 
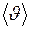– средняя скорость теплового движения молекул; 
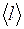– средняя длина свободного пробега.
Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное взаимное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей или твёрдых тел. В химически чистых газах при постоянной температуре диффузия возникает вследствие неодинаковой плотности в различных частях объёма газа. Для смеси газов диффузия вызывается различием в плотностях отдельных газов в разных частях объёма смеси.
В химически однородном газе явление диффузии заключается в переносе массы газа из мест с большей плотностью газа в места с меньшей плотностью и подчиняется закону Фика
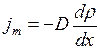, (I.44)
где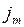 
– плотность потока массы – величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х.
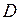– коэффициент диффузии;
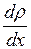– градиент плотности, равный скорости изменения плотности на единицу длины х в направлении нормали к этой площадке.
Знак минус показывает, что перенос массы происходит в направлении убывания плотности, поэтому знак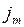и и 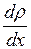противоположны. Коэффициент диффузии 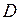численно равен плотности потока массы при градиенте плотности, равном единице. Согласно кинетической теории газов, коэффициент диффузии можно рассчитать по формуле
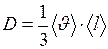. (I.45)
Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.
Сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона
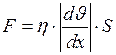, (I.46)
где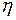 
- динамическая вязкость (коэффициент вязкости) (приложение Б., таблица Б.9);
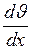– градиент скорости, показывающий быстроту изменения скорости в направлении оси х, перпендикулярном направлению движения слоёв;
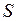– площадь, на которую действует сила 
.
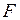Взаимодействие двух слоёв согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передаётся импульс, по модулю равный действующей силе. Тогда выражение (I.46) можно представить в виде
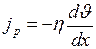, (I.47)
где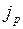 
– плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную данной оси.
Знак минус указывает, что импульс переносится в направлении убывания скорости, поэтому знак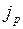и и 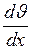противоположны.
Динамическая вязкость 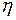– численно равна плотности потока импульса при градиенте скорости, равном единице.
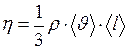. (I.48)
Из сопоставления формул (I.42), (I.44) и (I.47), описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой.
Между коэффициентами явлений переноса имеются простые зависимост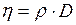и
и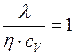 
. (I.49)
Дата добавления: 2016-09-06; просмотров: 6122;
Поиск по сайту
Узнать еще
- I.3.9 ТЕПЛОВЫЕ ЯВЛЕНИЯ В СРЕДАХ ПРИ МЕХАНИЧЕСКОМ ВОЗДЕЙСТВИИ
- II. Выявление причин появления события.
- А. Причины появления и способа уменьшения нелинейных искажений
- Адгезионные явления
- Анализ внешних факторов с целью выявления причин кризиса.
- Аналогия явления переноса субстанций. Законы молекулярного переноса
- Безработица: причины появления и виды безработицы в экономике.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
