Теплопроводность газов

Явление возникновения потока тепла в газе (или любом другом веществе) называется теплопроводностью. Перенос количества теплоты можно описать с помощью потока теплоты.

Потоком теплоты называется количество теплоты, перенесённое через площадку, перпендикулярную направлению переноса, в единицу времени. Плотность потока теплоты, как количество теплоты, перенесённое через единичную площадку, перпендикулярную направлению переноса, в единицу времени, можно выразить так:

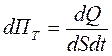(14.14)

Основной закон теплопроводности – закон Фурье: плотность потока теплоты прямо пропорциональна градиенту температуры со знаком «минус»:

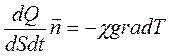(14.15)

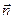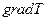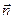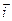Здесь - вектор положительной нормали к площадке dS, через которую переносится количество теплоты, его направление совпадает с направлением переноса количества теплоты, - градиент температуры, направлен в сторону наиболее быстрого возрастания температуры, χ- коэффициент теплопроводности. Для одномерного случая, когда направления векторов и совпадают:

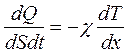(14.16)

Коэффициент теплопроводности численно равен потоку теплоты при единичном градиенте температуры. Для идеальных газов он может быть выражен так:

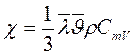(14.17)

Здесь С_mV – удельная теплоёмкость при постоянном объёме. Коэффициент теплопроводности прямо пропорционален 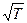и не зависит от давления. В СИ коэффициент теплопроводности измеряется в .

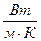Теплопроводность бывает стационарной, когда градиент температуры поддерживают постоянным, и нестационарной, при которой градиент температуры изменяется. Нестационарная теплопроводность приводит к выравниванию температур разных частей газа. Разность температур со временем убывает по экспоненциальному закону:

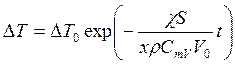(14.18)

Здесь 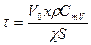- время релаксации, то есть время, в течение которого между двумя объёмами газа уменьшается в е раз; x – расстояние, на котором определяется разность температур; S – площадь, через которую переносится количество теплоты; 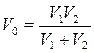- приведённый объём; V₁ – объём области с температурой T₁; V₂ – объём области с температурой T₂, определяющих разность температур .

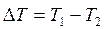Описанные выше явления переноса имеют много общего с формальной точки зрения. Во-первых, уравнения, выражающие основной закон переноса, формально имеют одинаковый вид. Во-вторых, во всех случаях имеется какая-нибудь переносимая величина, при возникновении градиента некоторых величин. Направление переноса потоков связано с градиентами величин знаком «минус». В. третьих, все рассмотренные явления переноса справедливы при слабом нарушении равновесного состояния системы.

Явления переноса в жидкостях и твёрдых телах формально можно описать с помощью аналогичных уравнений переноса. Однако механизм переноса в них отличается от механизма переноса в идеальных газах и выражения коэффициентов переноса невозможны в том же виде, что и для идеальных газов, поскольку для жидкостей и твёрдых тел, где нельзя пренебречь взаимодействием между молекулами, бессмысленно понятие средней длины свободного пробега.

ЛИТЕРАТУРА

1 Савельев И.В. Курс общей физики: В 3 т. – М.: Наука, 1989.

2 Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высш. шк., 1989. – 608 с.

3 Курс физики: Учеб. для вузов: В 2 т. Т.1 / Под ред. В.Н. Лозовского. – СПб.: Издательство «Лань», 2001. – 576 с.

4 Ремизов А.Н., Потапенко А.Я. Курс физики: Учеб. для вузов. – М.: Дрофа, 2002. – 720 с.

5 Трофимова Т.И. Курс физики: Учеб. пособие для вузов. – М.: Высш. шк., 1990. – 478 с.

6 Трофимова Т.И. Краткий курс физики: Учеб. пособие для вузов. – М.: Высш. шк., 2004. – 352 с.

7 Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики с решениями: Учеб. пособие для вузов. – М.: Высш. шк., 1999. – 591 с.

8 Физический энциклопедический словарь / Гл. ред. А.М. Прохоров. Ред. кол. Д.М. Алексеев, А.М. Бонч-Бруевич, А.С. Боровик-Романов и др. – М.: Сов. энциклопедия, 1984. – 944 с.

9 Енохович А.С. Справочник по физике и технике: Учеб. пособие для учащихся. – М.: Просвещение, 1989. – 224 с.

10 Дмитриева В.Ф. Физика: Учебник для студ. образоват. учреждений сред. проф. Образования. – М.: Издат. центр «Академия», 2003. – 464 с.