Основное уравнение молекулярно-кинетической теории

Основное уравнение молекулярно-кинетической теории идеального газа связывает макроскопический параметр газа с микроскопическими характеристиками, относящимися к его структурным элементам - молекулам. Учитывая беспорядочное непрерывное движение молекул и их соударения со стенками сосуда и друг с другом, макроскопическим параметром может быть давление газа, которое связано с изменением импульса молекул (микроскопический параметр).

Как известно, величина давления определяется силой, действующей перпендикулярно на единицу площади поверхности:

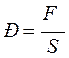. (11.1)

Давление газа на стенки обусловлено огромным числом столкновений молекул газа со стенками, согласно второму закону Ньютона:

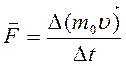(11.2)

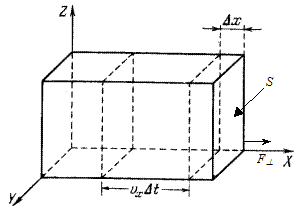
Рисунок 11.1 – К выводу основного уравнения МКТ

Импульс одной молекулы: вдоль оси Х равен 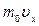, где m₀ - масса одной молекулы. Пусть в единице объема прямоугольного сосуда (рисунок 11.1) находится n молекул, из них половина движется вдоль оси Х, а другая половина - в противоположном направлении. За время Dt в слой Dx (Dx – расстояние, на котором проявляется действие молекул на стенку) слева направо входит 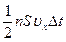молекул. Каждая из них обладает импульсом 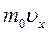, следовательно, общий импульс, вносимый ими в слой, равен:

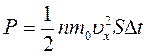. (11.3)

За это же время слой покидает, двигаясь, справа налево, такое же число молекул с таким же общим импульсом, но противоположного знака. Общее изменение импульса:

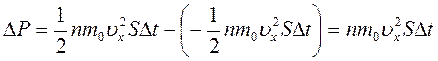. (11.4)

Импульс силы, действующей на стенку, площадью S, равен изменению импульса частиц 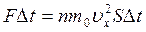. Тогда давление на стенку, будет определяться формулой:

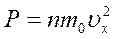(11.5)

Двигаясь беспорядочно в пространстве, молекулы имеют составляющие скоростей и вдоль других осей. Полная скорость молекулы может быть выражена через её составляющие по трём независимым направлениям : .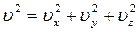

Поскольку в движении участвует множество молекул, то необходимо использовать средние квадраты скоростей:

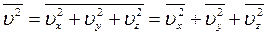. (11.6)

Так как движение беспорядочное, то все три компоненты скоростей равноправны 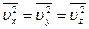. Отсюда 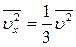. После подстановки в уравнение (11.5) получим:

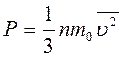(11.7)

Уравнение (11.7) связывает макроскопический параметр давление и микроскопические – массу и средний квадрат скорости молекулы, поэтому его можно считать основным уравнением МКТ идеальных газов. Однако, часто это уравнение используют в другом виде:

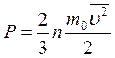. (11.8)

Здесь 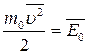– средняя кинетическая энергия поступательного движения молекулы. Таким образом, давление идеального газа определяется средней кинетической энергией поступательного движения молекулы и является среднестатистической величиной

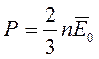(11.9)