Вязкость жидкости и методы ее измерения

Идеальная жидкость, т.е. жидкость, движущаяся без трения, является абстракцией. Всем реальным жидкостям и газам в большей или меньшей степени присуща вязкостьили внутреннее трение. Вязкость проявляется в том, что возникающее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается.

Рассмотрим поток среды (жидкости или газа), скорость течения в которой различна в разных местах. Такое состояние вещества не является равновесным, и в нем будут происходить процессы, стремящиеся выровнять скорость течения. Эти процессы называютсявнутренним трением.При внутреннем трении благодаря тепловому движению молекул происходит передача импульса от более быстрых участков потока к менее быстрым.

Предположим, что жидкость течет везде в одном направлении, т.е. вектор скорости течения 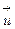имеет постоянное значение вдоль всего потока направления. Предположим, что величина скорости 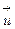меняется только вдоль одного направления, перпендикулярного направлению скорости:

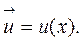
Введем понятие о потоке импульса: это есть полный импульс, переносимый в 1 сек. В положительном направлении оси х через единичную площадку, перпендикулярную к оси х; обозначим этот поток 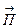. Можно утверждать, что поток импульса пропорционален градиенту скорости течения u:

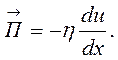(9.8)

Величина η называется коэффициентом вязкости среды. Коэффициент вязкости определяет быстроту передачи импульса из одного потока в другое. Скорость же равна импульсу, деленному на массу. Поэтому быстрота выравнивания скорости потока будет определятся величиной η/ρ, где ρ – плотность, т.е. масса единицы объема жидкости. Величину

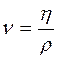(9.9)

называют кинематической вязкостью, в отличие от самого коэффициента η, называемого в этой связи динамической вязкостью.

Предположим, что жидкость течет, соприкасаясь с твердой поверхностью (жидкость, текущая вдоль стенок трубы). Скорость течения обращается в ноль на стенке. По мере удаления от стенки в глубь жидкости ее скорость увеличивается и, благодаря вязкости, возникает поток импульса по направлению из жидкости к стенке.

С другой стороны, изменение импульса тела со временем есть сила, действующая на тело. Поэтому импульс 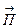, переносимый в единицу времени через единицу поверхности и передаваемый от жидкости к стенке, представляет собой силу трения, действующую на единицу поверхности твердой стенки со стороны протекающей мимо нее жидкости.

Явлением внутреннего трения (вязкости) называется появление сил трения между слоями газа или жидкости, движущимися друг относительно друга параллельно и с разными по величине скоростями. Слой, движущийся быстрее, действует с ускоряющей силой на более медленно движущийся слой. Наоборот, медленно движущийся слой тормозит более быстро движущийся слой газа или жидкости. Силы внутреннего трения, которые возникают при этом, направлены по касательной к поверхности соприкосновения слоев. Причиной вязкости является наличие упорядоченного движения газа или жидкости с различными скоростями и теплового хаотического движения молекул со скоростями, зависящими от температуры. Хаотическое движение молекул переносит их из слоя В, движущегося со скоростью 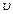₂, в слой А, движущийся со скоростью 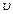₁ (рисунок 9.3).

При этом происходит перенос импульсов mν упорядоченного движения молекул. Если ν₁ > ν₂, то молекулы, ранее бывшие в слое В, оказавшись в слое А, при столкновении с его молекулами ускоряют свое упорядоченное движение, а упорядоченно движущиеся молекулы слоя А замедляются.

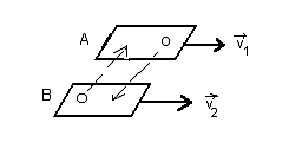
Рисунок 9.3 – К пояснению причин возникновения вязкости

Наоборот, при переходе молекул из быстрее движущегося слоя А в слой В они переносят большие импульсы mν₁ и межмолекулярные соударения в слое В ускоряют движение молекул этого слоя.

Явление внутреннего трения описывается законом Ньютона:

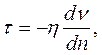(9.10)

где τ – напряжение трения, т.е. физическая величина, численно равная силе внутреннего трения, действующей на единицу площади поверхности слоя; dν/dn – градиент скорости – изменение скорости движения слоев на единицу длины в направлении внутренней нормали n к поверхности слоя.

Коэффициент внутреннего трения не зависит от давления (или плотности) газа или жидкости, поскольку 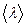~ 1/ρ. Объясняется это тем, что при изотермическом увеличении плотности газа, например, в 2 раза, вдвое увеличивается число переносчиков импульса, но каждая молекула (атом) проходит без столкновения вдвое меньшее расстояние и переносит вдвое меньший импульс. Поэтому в целом перенос импульса не меняется.

При исследовании различных вопросов о движении жидкости большое значение приобретают простые методы, основанные на соображениях размерности тех физических величин, от которых это движение может зависеть. Рассмотрим, например, равномерное движение твердого шара через жидкость; задача заключается в определении испытываемой шаром силы сопротивления F.

Физические свойства жидкости, определяющие ее течение или движение в ней посторонних тел, характеризуются всего двумя величинами: ее плотностью ρ и коэффициентом вязкости η. Кроме того, в рассматриваемом случае движение зависит еще от скорости шара u и от его радиуса а. Таким образом, в нашем распоряжении имеется всего четыре параметра со следующими размерностями: ρ[кг/м³]; η [кг/м сек]; u [м/сек]; a[м]. Составим из них безразмерную величину. Исключить размерность [кг] можно лишь одним способом: η/ρ, т.е. образовав отношение ν = η/ρ с размерностью [ν] = м²/сек. Далее, для исключения [сек]: [u/ν] = 1/м. Теперь эту дробь умножаем на а:

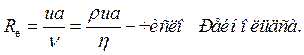
Это число является очень важной характеристикой движения жидкости. Под величиной а в числе Рейнольдса надо понимать какой-либо линейный размер тела заданной формы. При этом мы получаем возможность сравнивать течения жидкости вокруг геометрически подобных тел, отличающихся своими размерами.

Для измерения вязкости (вискозиметрии) применяют ряд экспериментальных методов, основанных на различных принципах. Каждый из этих методов обладает особым диапазоном условий его применения.

Независимо от применяемого метода для корректных измерений вязкости необходимо соблюдение следующих требований: 1) результат измерений должен зависеть от линейных размеров рабочих элементов вискозиметра; 2) не должно иметь место пристеночное скольжение в жидкости; 3) поток жидкости в вискозиметре должен быть ламинарным, т.е. в капиллярах необходимо значение числа Рейнольдса Re < 2320, а в случае падающего шарика – Re < 1.

Абсолютное измерение вязкости гарантируют капиллярный, ротационный методы и метод падающего шарика. В остальных случаях необходимо прибегать к помощи калибровочных жидкостей с известными значениями вязкости.

Раздел 2 Молекулярная физика и термодинамика

Лекция 10 Молекулярно-кинетические представления

о веществе

10.1 Предмет и методы молекулярной физики

10.2 Основные положения МКТ

10.3 Размеры и масса молекул, количество вещества

11.4 Модель идеального газа

10.1 Предмет и методы молекулярной физики

Молекулярная физика изучает физические свойства макроскопических тел (твердых, жидких, газообразных), а также происходящие в них физические процессы, обусловленные тепловым движением и взаимодействием микрочастиц (атомов, молекул, ионов), составляющих эти тела. Под макроскопическими телами следует понимать тела, состоящие из большого числа атомов или молекул.

Существует два подхода к изучению макроскопических систем: статистический и термодинамический. Поэтому молекулярная физика делится на две большие части – молекулярно-кинетическую теорию и термодинамику.

Теория, объясняющая тепловые явления в макроскопических телах и внутренние свойства этих тел на основе представлений о том, что все тела состоят из отдельных, хаотически движущихся частиц, носит название молекулярно – кинетической теории (МКТ).Она оперирует статистическими методами, характеризующими движение огромной совокупности частиц.

Термодинамика (ТД) занимается изучением различных свойств тел и изменений состояния вещества без учета микроскопической картины. В основе ТД лежат несколько фундаментальных законов (начал), установленных на основании обобщения большой совокупности опытных данных. МКТ и ТД позволяют глубоко изучить и понять многие явления природы.

Как уже отмечалось выше, молекулярная физика изучает физические свойства макроскопических систем (тел). Предметом её изучения являются молекулярные формы движения больших совокупностей молекул (систем).

Системой называют конечную область пространства с находящимися в ней физическими объектами исследования. Граница системы может быть как материальной (стенки сосуда), так и воображаемой; неподвижной или движущейся; проницаемой или непроницаемой. Система характеризуется не только особенностями своей границы, но и физическими или химическими свойствами вещества, находящегося в занимаемой системой области пространства.

Макроскопическими системами называют системы, содержащие большое количество физических объектов. Термодинамические макроскопические системы содержат большое количество молекул (атомов, ионов). Различают разные виды термодинамических систем (ТС): закрытые, открытые, адиабатные и изолированные.

Закрытые ТС это системы, не обменивающиеся веществом с другими системами.

Открытые ТС это системы, обменивающиеся веществом и энергией с другими системами.

Адиабатные ТС это системы, в которых нет теплообмена с другими системами.

Изолированные ТС это системы, не обменивающиеся с другими системами ни энергией, ни веществом.

Для описания макросистем в молекулярной физике используют основные параметры состояния – температуру, давление, объём. Любое теоретическое описание реальных систем возможно только на основе той или иной модели, в которой учитывают определённые особенные свойства, а второстепенными пренебрегают. В молекулярной физике рассматривают следующие основные модели: идеальный газ, реальный газ, идеальная жидкость, реальная жидкость, твердое тело, плазма.

Макросистемы могут находиться в равновесном и неравновесном состоянии.

Равновесными состояниями называют такие, при которых макроскопические величины, описывающие поведение изолированной системы, остаются неизменными во времени и одинаковыми в пространстве.

В неравновесном состоянии макровеличины, характеризующие состояние системы, изменяются в пространстве и во времени, при этом в системе возникают потоки вещества и энергии (явления переноса).

Неравновесные состояния сложных систем изучают, используя методы физической кинетики.

Макроскопические системы могут быть линейными и нелинейными. В слабо неравновесных состояниях, где градиенты величин малы, переносимые потоки и силы, вызывающие их, линейно зависят от градиентов. В сильно неравновесных состояниях, где градиенты величин велики, потоки являются более сложными функциями градиентов.

При изучении состояния систем используют термодинамический и статистический методы.

Термодинамический метод. Систему рассматривают без учета её внутренней структуры. При этом используют понятия и величины, относящиеся к системе в целом. Например, идеальный газ в состоянии равновесия характеризуют объёмом, давлением и температурой (V, P и T). Экспериментально устанавливают связь между этими величинами. Для термодинамического подхода характерно использование термодинамических потенциалов для описания систем, находящихся в равновесном или слабо неравновесном состоянии. Для сильно неравновесных нелинейных систем описание состояния через потенциалы невозможно.

Статистический метод. Динамическое описание системы, содержащей большое число частиц, невозможно. Для изучения макросистем применяют статистические методы, использующие понятия и величины, относящиеся не к отдельным частицам, а к большим совокупностям частиц. Законы поведения совокупностей большого числа частиц, использующие статистические методы, называются статистическими закономерностями. Эти закономерности, как и величины, описывающие состояние системы, зависят от того, в каком состоянии находится система: равновесном или неравновесном.

10.2 Основные положения МКТ

Представление о том, что все тела состоят из мельчайших, обособленных частиц – атомов, возникло еще в глубокой древности и было впервые высказано греческим философом Демокритом в V в. до н.э. Затем эти воззрения были забыты и возрождены лишь во второй половине XVII в. Р. Бойлем, а далее в XVIII – XIX вв. разработаны М.В. Ломоносовым, Д. Дальтоном, А. Больцманом, Д.К. Максвеллом и др. в качестве научной теории.

Молекулярно-кинетическая теория основана на трех основных положениях: