Распределение молекул по скоростям и энергиям

Распределение Максвелла.При изучении газов принята основная модель — модель идеального газа как большого коллектива невзаимодействующих частиц, непрерывно участвующих в беспорядочном тепловом движении. К этому коллективу частиц применим статистический метод, базирующийся на математиче­ской теории вероятностей, на понятиях о средних, среднеквадратичных и наиболее вероятных параметрах, характеризующих поведение частиц в коллективе.

Рассмотрим распределение Максвелла или распределение молекул по скоростям.

Скорости молекул газа имеют различные значения и направления,
причем как величина, так и направление скорости каждой отдельной молекулы изменяются в результате соударений, поэтому нельзя определить

число молекул, обладающих точно заданной скоростью в данный момент времени, но можно подсчитать число молекул, скорости которых лежат в интервале от 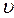до .

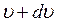При этом предполагается, что в газе не существует молекул, имею­щие в точности одинаковые скорости, и число молекул dN, скорость которых лежит в узком интервале между 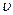и 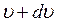пропорционально общему числу молекул N, ширине интервала 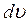и зависит от скорости 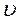. Такаятеоретическая зависимость была установлена Максвеллом на осно­вании теории вероятностей:

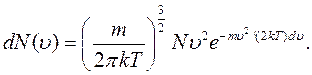(11.11)

Функцию

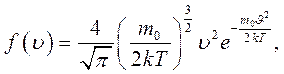(12.12)

показывающую относительное число молекул, скорость которых лежит в интервале скоростей 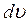, называют функцией распределения молекул газа по скоростям.Графически эта функция представлена на рисунке 11.1.

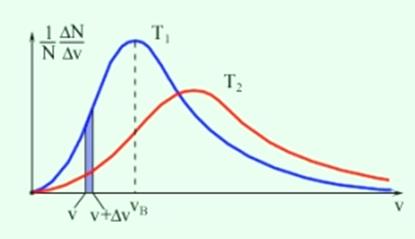
Рисунок 11.1 – Вид распределения Максвелла для различных температур

Заштрихованная область соответствует относительному числу молекул газа, скорости которых лежат в интервале от 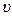до 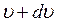. Максимум кривой распределения соответствует наиболее вероятной скорости молекул 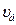, которую можно найти, исследовав на максимум функцию f( 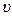). Беря производную от (12.2) по скорости и приравнивая ее нулю, легко получить выражение для наиболее вероятной скорости молекул.:

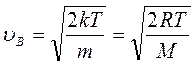(11.13)

Вид функции распределения f( 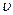)зависит от рода газа (массы моле­кул) и температуры Т. Давление и объем газа на распределение молекул по скоростям не влияют.

При повышении температуры (Т₂ > Т₁) 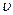_В возрастает, поэтому мак­симумы кривой распределения молекул по скоростям сдвигаются в сто­рону больших скоростей (рис. 12.1); следовательно, с ростом температуры возрастает относительное число молекул, обладающих большой скоростью.

Кроме наиболее вероятной ско­рости движение молекул газа характеризует средняя арифметическая скорость:

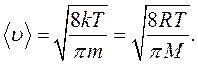. (11.14)

Средняя квадратичная скорость определяется как квадратный корень из среднего квадрата скорости и связана со средней кинетической энергией поступательного движения молекул. Чтобы найти её с помощью распределения Максвелла, нужно определить отношение суммы квадратов скоростей молекул, содержащихся в единице объёма, к числу молекул в этом объёме:

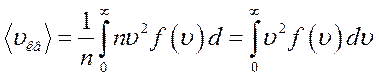
Для идеального газа, находящегося в состоянии термодинамического равновесия при температуре Т, она равна :

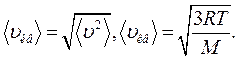(11.15)

Если все молекулы одинаковы по массе, то

.

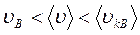Используя распределение молекул идеального газа по скоростям

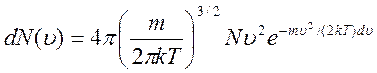
найдем распределение молекул газа по энергиям.

Молекулы идеального газа обладают кинетической энергией Е=1/2m 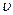², откуда следует, что

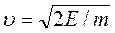и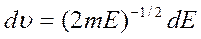

Переходя от переменной 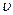к переменной Е, получаем

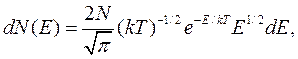(11.16)

где dN(E) — число молекул, имеющих кинетическую энергию, заключен­ную в интервале от Е до Е + dE.

Функция распределения молекул по энергиям имеет вид

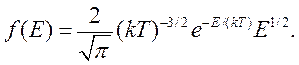(11.17)

Средняя кинетическая энергия молекулы идеального газа (Е) опре­деляется интегралом:

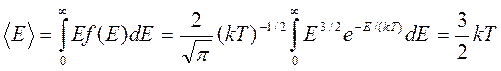. (11.18)

Закон распределения Больцмана. При рассмотрении закона распределения Максвелла предполагалось, что молекулы равномерно распределяются по всему объему сосуда, что справедливо, если объем сосуда небольшой.

Для больших объемов равномерность распределения молекул по объему нарушается из-за действия силы тяжести, вследствие чего плот­ность, а следовательно, и число молекул в единице объема будут неодинаковыми. Рассмотрим молекулы газа, находящегося в поле тяготения Земли.

Выясним зависимость давления атмосферы от высоты над поверхно­стью Земли. Допустим, на поверхности Земли (h = 0) давление атмосфе­ры р₀. На высоте h оно равно р. При увеличении высоты на dh давление уменьшится на dр:

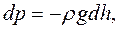
где р — плотность воздуха на данной высоте, р = тп₀, где m — масса моле­кулы, n₀ — концентрация молекул].

Используя соотношение р = п₀кТ, получаем

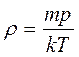
тогда

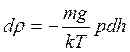(11.19)

Полагая, что на некоторой высоте h T= const, g = const, разделяя пе­ременные, интегрируем выражение (11.19):

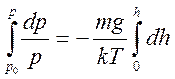
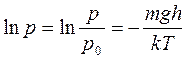
Получаем

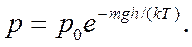(11.20)

Это, так называемая барометрическая формула. Барометрическая формула показывает зависимость давления газа от высоты над поверхностью Земли. Если учесть, что концентрация молекул воздуха в атмосфере определяет дав­ление, то формулу (11.20) можно записать в виде

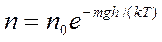(11.21)

Из формулы (11.21) следует, что с понижением температуры число частиц на высоте, отличной от нуля, убывает и при Т = О К обращается в нуль, т. е. при О К все молекулы расположились бы на земной поверх­ности.

Так как потенциальная энергия молекул на различной высоте раз­лична и на высоте h определяется по формуле Е„ = mgh, то

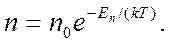(11.22)

Выражение (11.22) представляет собой закон Больцмана, показывающий распределение участвующих в теп­ловом движении молекул в потенциальном поле сил, в частности в поле силы тяжести.

Закон Больцмана является универсальным, он справедлив для любых частиц, находящихся в потенциальном поле сил. Он выражает условие равновесия между тепловым движением, стремящимся к максимальному рассеянию частиц, и действием внешних сил — сил тяжести, стремящих­ся к максимальному уплотнению частиц вблизи земной поверхности.

Экспериментальные подтверждения справедливости распределения Больцмана были получены при определении постоянной Авогадро.

Постоянная Авогадро была определена двумя независимыми спосо­бами. Первый способ основан на применении барометрической формулы к эмульсиям и суспензиям, находящимся в равновесном состоянии. Дру­гой способ был предложен Ж. Перреном и основан на наблюдении бро­уновского движения. Эти два способа дали одинаковые результаты. По­стоянная Авогадро, т. е. число молекул в 1 моль вещества, равна 6,023 10²³ моль^-1.