Центробежные силы инерции

Рассмотрим вращающийся диск с закрепленными на нем стойками с шариками, подвешенными на нитях (рисунок 6.7). При вращении диска с постоянной угловой скоростью 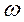шарики отклоняются на некоторый угол, тем больший, чем дальше он находится от оси вращения. Относительно инерциальной системы отсчета (неподвижной) все шарики движутся по окружности соответствующего радиуса R, при этом на шарики действует результирующая сила 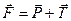(рисунок 6.7).

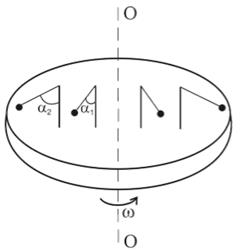
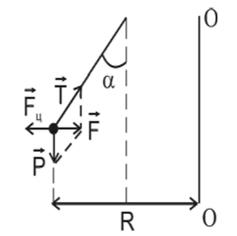
Рисунок 6.7 – К выводу центробежной силы инерции

Согласно второму закону Ньютона

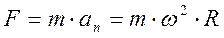. (6.18)

С учетом того, что 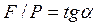, можно записать

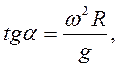
т.е. угол отклонения шарика зависит от угловой скорости и от его удале­ния от оси вращения диска.

Относительно неинерциальной системы отсчета, связанной с вра­щающимся диском, шарик находится в покое.

Это возможно в том случае, если сила 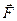(6.18) уравновешена силой инерции 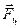называемой центробежной силой инерции:

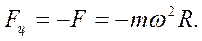(6.19)

Центробежные силы, как и всякие силы инерции, существуют только в ускоренно движущихся(вращающихся) системах отсчетаи исчезают при переходе к инерциальным системам отсчета.

Действию центробежной силы подвергается, например, пассажир в движущемся автобусе на поворотах. Если в центробежной машине подве­сить на нитях несколько шариков и привести машину в быстрое вращение, то центробежные силы инерции отклонят шарики от оси вращения. Угол отклонения тем больше, чем дальше шарик отстоит от оси. Центробежные силы используются в центробежных сушилках для отжима белья, в сепа­раторах для отделения сливок от молока, в центробежных насосах, цен­тробежных регуляторах и т.д. Их надо учитывать при проектировании быстровращающихся деталей механизмов.

Сила Кориолиса

При движении тела относительно вращающейся системы отсчета, кроме центробежной силы, появляется еще одна сила, называемая силой Кориолиса.

Рассмотрим шарик массой m, движется прямолинейно со скоростью 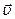от центра к краю диска (рисунок 6.8). Если диск неподвижен, то шарик попадает в точку М, а если диск вращается с постоянной угловой скоростью , то шарик попадает в точку N. Это обусловлено тем, что на шарик действует сила Кориолиса.

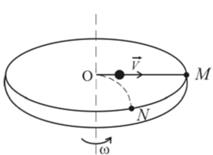
Рисунок 6.8 – Действие силы Кориолиса на шарик

Появление силы Кориолиса можно обнаружить, если рассмотреть пример с шариком на спице на вращающемся диске, но без пружины. Для того чтобы заставить шарик двигаться с некоторой скоростью 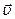вдоль спицы, необходима боковая сила. Шарик вращается вместе с диском с по­стоянной угловой скоростью , поэтому его момент импульса равен:

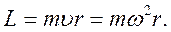(6.20)

Если шарик будет перемещаться вдоль спицы с постоянной скоро­стью 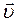то с изменением расстояния от центра момент импульса шарика изменится. Для того чтобы заставить шарик двигаться по вращающемуся диску вдоль радиальной прямой со скоростью 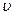, необходимо прилагать боковую силу направленную перпендикулярно его движению (рисунок 6.9).

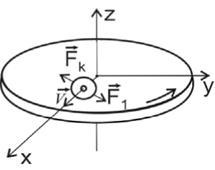
Рисунок 6.9 – К выводу силы Кориолиса

Относительно вращающейся системы (диска) шарик движется с постоянной скоростью. Это можно объяснить тем, что сила 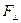уравновешивается приложенной к шарику силой инерции 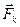, перпендикулярной к скорости шарика.

Сила 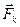и есть Кориолисова сила инерции. Она определяется выражением

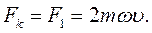(6.21)

С учетом направления силу Кориолиса 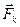можно представить в виде

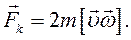(6.22)

Сила Кориолиса всегда перпендикулярна скорости тела 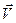. Во вра­щающейся системе отсчета при 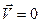эта сила отсутствует. Таким обра­зом, Кориолисова сила инерции возникает только тогда, когда система от­счета вращается, а тело движется относительно этой системы. Действием силы Кориолиса объясняется ряд эффектов, наблюдающихся на поверхности Земли, например, поворот плоскости колебаний маятника Фуко относительно Земли, отклонение к востоку от линии отвеса свободно падающих тел, размытие правого берега рек в северном полушарии и левого в южном, неодинаковый износ рельсов при двухколейном движении.