Кинетическая энергия

Преобразуем выражение для работы, пользуясь основным уравнением динамики и выражением для пути :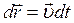

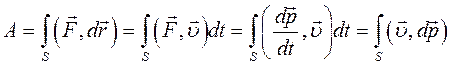. (4.7)

Скалярное произведение под интегралом можно представить:

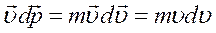. (4.8)

Подставляя (4.8) в (4.7) и рассматривая работу на конечном участке пути от точки 1 до точки 2, получаем:

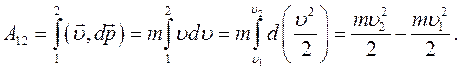(4.9)

Из последнего выражение следует, что работа постоянной силы, действующей на тело равна разности энергий в двух состояниях.

Физи­ческая величина, равная полови­не произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

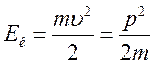. (4.10)

Таким образом, работа силы при перемещении материальной точки из положения 1 в 2 равна изменению кинетической энергии этой точки

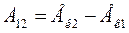. (4.11)

Для системы частиц: кинетическая энергия всей системы материальных точек равна сумме кинетических энергий:

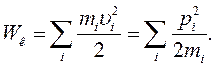(4.12)

Отметим важный момент: кинетическая энергия определяется работой не только внешних, но и внутренних сил. Этим кинетическая энергия отличается от импульса, который меняется только за счет внешних сил (внутренние силы не меняют импульса всей системы).