Математическое введение к алгебраическим кодам
В настоящее время наиболее изучены, многочисленны, исследованы и широко используются корректирующие коды, описываемые при помощи аппарата высшей алгебры. Поэтому, прежде чем приступить к рассмотрению конкретных корректирующих кодов ознакомимся с используемой при этом частью высшей алгебры.
Предметом высшей алгебры являются так называемые алгебраические системы, являющиеся совокупностью некоторых множеств и определенных на элементах этих множеств операций.
Под двухместной операцией здесь понимается однозначное сопоставление двум элементам множества с третьим по определенным правилам.
Под одноместной операцией понимается однозначное сопоставление одному элементу множества с другим по определенным правилам.
Обычно основные операции называются сложением (a+b=c) и умножением (ab=d), а обратные им вычитанием и делением, даже если этим операции производятся не над числами (например, над оттенками цветов или геометрическими фигурами) и не идентичны соответствующим арифметическим операциям. С точки зрения высшей алгебры элементарная школьная алгебра − одна из бесконечного множества других возможных алгебраических систем.
Свойства и наименования систем зависят от законов, которые в них определены.
Пусть S – множество некоторых элементов, а а и b - элементы, принадлежащие множеству S (последнее записывается в виде 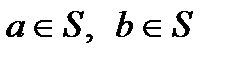 ).
).
В таблице 3.9 определены некоторые важные для нас законы (Элементы теории передачи дискретной информации. –М.:Связь, 1972):
Таблица 3.9.
| Законы композиции | Операция | |||
| Сложение | Умножение | |||
| Обозн. | Формула | Обозн. | Формула | |
Замкнутость (если 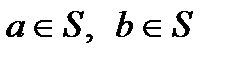 , то , то 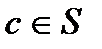 ). ).
| А1 | a+b=c | M1 | ab=c |
| Ассоциативность | А2 | (a+b)+c= a+(b+c) | M2 | (ab)c=a(bc) |
| Коммутативность | А3 | a+b=b+a | M3 | ab=ba |
| Наличие нулевого для операции сложения и единичного для операции умножения элемента е. | А4 | a+e=e+a=a | M4 | ae=ea=a |
Наличие для 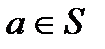 обратного элемента обратного элемента 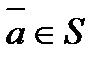 . .
| А5 | 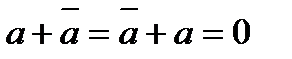
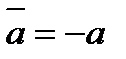
| M5 | 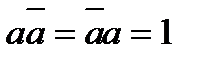 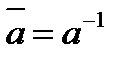
|
| Дистрибутивность | D1 | a(b=c) = ab=ac | ||
| D2 | (b+c)a = ba+bc |
Система, в которой определены две основные операции (сложение и умножение) и которая соответствует всем отмеченным в таблице свойствам, называется полем.
Система, в которой определены обе основные операции и выполняются законы А1−А5, М1, М2, D1 и D2, называется кольцом.
Если дополнительно в некотором кольце выполняется закон М3, то это кольцо – коммутативное.
Система, в которой задана лишь одна операция (сложение или умножение) и выполняются законы А1, А2, А4, А5 или М1, М2, М4, М5 называется группой.
Если в группе определена операция сложения, то такая группа называется аддитивной, если умножения, то мультипликативной.
Группа называется коммутативной или абелевой, если в ней выполняется закон коммутативности (А3 или М3) в зависимости от введенной операции.
Группы, имеющие конечное число элементов, называются конечными.
Построим алгебраическую систему, удобную для описания кодов равномерных двоичных кодов.
Предположим, что кодовые комбинации образуют множество S. Определим теперь операцию суммирования, обладающую свойствами А1, А2, А4, А5 и образуем таким образом группу. Операцию суммирования определим таким образом, чтобы удовлетворялось условие замкнутости А1. Следовательно, число разрядов при выполнении этой операции меняться не должно. Этому условию отвечает операция поразрядного сложения кодовых слов по модулю 2 (обозначается знаком  ). Результатом такого сложения будет 1, если число единиц в разряде слагаемых четно, и 0 − если нечетно.
). Результатом такого сложения будет 1, если число единиц в разряде слагаемых четно, и 0 − если нечетно.
Пример:
1 0 1 1 1 0 1
 0 1 1 1 1 0 1
0 1 1 1 1 0 1
0 0 0 1 1 1 0
1 1 0 1 1 1 0
Выбранная операция коммутативна, поэтому группа будет абелевой.
Нулевым элементом является комбинация, состоящая из одних нулей (это легко проверить).
Противоположным элементом является сама кодовая комбинация, а обратная операция – вычитание – тождественна основной операции суммирования.
Линейные коды
Рассмотрим класс алгебраических кодов, называемых линейными.
Определение: Линейными называют блоковые коды, дополнительные разряды которых образуются путем линейных операций над определенными информационными разрядами.
Здесь используется понятие линейная операция.
Линейной операцией называется операция над объектами, описываемая выражением: С0 + С1Х1 + С2Х2 + … , где Сi – константы, Хi – объекты.
Слово линейный здесь используется в виду того, что вышеприведенное выражение описывает многомерную прямую линию. Следует только иметь в виду, что операции умножения и сложения, указанные в этом выражении, могут отличаться от привычных арифметических. В теории кодирования в качестве операции сложения используется сложение по модулю 2 (  ).
).
Дата добавления: 2021-04-21; просмотров: 536;











