Классификация кодов

1. В зависимости от способности обнаруживать и исправлять ошибки, различают коды, обнаруживающие ошибки, и коды, исправляющие ошибки. Первые позволяют только обнаруживать, но не исправлять ошибки. Вторые – не только обнаруживать, но и исправлять большую или меньшую долю обнаруженных ошибок.

2. По форме внесения избыточности различают разделимые инеразделимые коды.

В разделимых кодах кодовые слова четко разделены на две части. Одна часть состоит из исходных (кодируемых) разрядов, а другая из дополнительных разрядов, благодаря которым собственно и обеспечивается возможность обнаружения и/или исправления ошибок.

Ясно, что эти дополнительные разряды создают в сообщении избыточность (вспомним, что предполагается нулевая избыточность исходного (кодируемого) сообщения).

В кодовых словах неразделимого кода такое разделение отсутствует.

3. В зависимости от способа образования дополнительных разрядов разделимые коды подразделяются на систематические и несистематические. В систематических кодах дополнительные разряды символы образуются с помощью различных линейных операций над информационными. Систематические коды - самая обширная и наиболее применяемая группа корректирующих кодов.

4. По способу кодирования различают блочные и непрерывные коды.

При блочном кодировании входное кодируемое сообщение разбивается на блоки фиксированной длины k. Этим блокам ставятся в соответствие кодовые слова длиной n (n>k).

При непрерывном кодировании каждый символ b выходной последовательности (закодированного сообщения) определяется рекуррентным соотношением, связывающим его с соответствующими символами a входной последовательности (кодируемого сообщения), например: ,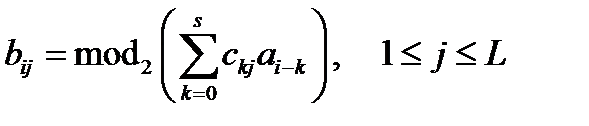

где: a – символы входной последовательности (кодируемого сообщения);

b – символы выходной последовательности (закодированного сообщения);

c_kj и s – константы, зависящие от кода;

i – номер символа входной последовательности (кодируемого сообщения);

j – номер символа в группе символов выходной последовательности (закодированного сообщения), создаваемой в результате поступления нового символа входной последовательности.

L – количество символов выходной последовательности, создаваемых в результате кодирования в ответ на поступления на вход кодера одного символа входной последовательности.

Следующим рисунком иллюстрируется кодирование непрерывным кодом:

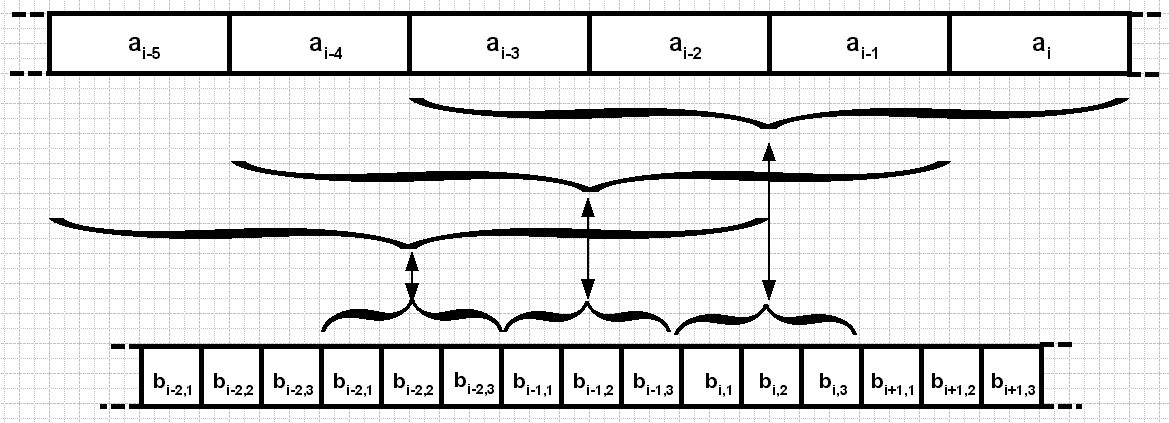
Рис. 3.4. Образование непрерывного кода.

Таким образом, на каждый символ входной последовательности приходится L символов выходной.

Существуют и другие варианты формулы кодирования.

5. По способу описания выделяют алгебраические коды, т.е. коды, описываемые с помощью аппарата высшей алгебры.

6. В зависимости от длины кодового слова различают равномерные и неравномерные коды. Если длина кодовых слов постоянна, код равномерный. В противном случае – неравномерный.

7. Рассмотрим блочный равномерный код. Если произвольная линейная комбинация кодовых слов – также кодовое слово, такой код называется линейным.

Одни и тот же код может одновременно принадлежать нескольким классам, например, может существовать алгебраический разделимый неравномерный код.