Общие принципы использования избыточности

Для простоты рассмотрим блоковый код. С его помощью каждым k разрядам (буквам) входной последовательности ставится в соответствие n-разрядное кодовое слова. Количество разного вида k-разрядных информационных комбинаций равно 2^k. Каждой из них ставится в соответствие определенное кодовое слово. Их также 2^k. Эти кодовые слова называются разрешенными.

Однако возможное число n-разрядных комбинаций равно 2ⁿ. Если из этого числа исключить все разрешенные кодовые слова, то останутся запрещенные кодовые слова.

Кодер посылает в линию связи только разрешенные кодовые слова, однако под действием помех они могут превратиться в любое другое из 2ⁿ возможных − в другое разрешенное или в запрещенное. Все запрещенные слова данного кода заранее известны. Поэтому факт получения такого кодового слова легко устанавливается и является верным признаком наличия в кодовом слове ошибки – ошибка обнаруживается.

Возможность исправления ошибки связана со свойством кода, называемого кодовым расстоянием.

Определить кодовое расстояние невозможно без предварительного определения другого понятия – расстояние между кодовыми словами.

Под расстоянием между кодовыми словами понимают количество различий в одноименных разрядах двух кодовых слов.

Если, например, одно кодовое слово имеет вид 011101001, а другое – 111001100, то расстояние между ними можно вычислить, выполнив операцию XOR (исключенное или) и подсчитав количество единичных разрядов в результате:

0 1 1 1 0 1 0 0 1

XOR

1 1 1 0 0 1 1 0 0

_______________________________________________

1 0 0 1 0 0 1 0 1

Расстояние между кодовыми словами, как видим, равно 4. Ниже будем расстояние между кодовыми словами обозначать буквой d. В данном примере d=4.

Вспомним, что весом кодового слова двоичного кода называют число единичных разрядов в нем. Тогда кодовое расстояние равно весу поразрядной суммы по модулю 2 кодовых слов, расстояние между которыми определяется.

Выше мы показали, что наиболее вероятными в случае ДСМК являются однократные ошибки, и, чем выше кратность ошибки, тем менее она вероятна. Возникновение ко-кратной ошибки можно трактовать как преобразование передаваемого кодового слова в другое, находящееся на расстоянии ко от передаваемого. Ясно, что переводы на меньшие расстояния более вероятны.

Геометрически множество разрешенных кодовых слов условно можно отобразить в виде точечного множества (рис. 3.7).

Рис. 3.7. Точечное множество.

Теперь можно определить понятие кодового расстояния.

Кодовым расстоянием данного кода называют наименьшее расстояние между разрешенными кодовыми словами этого кода. Ниже оно обозначается d_min.

В литературе по кодированию кодовое расстояние еще называют Хэминговым – по фамилии ученого, впервые его предложившего.

Продолжим изучение общих принципов использования избыточности.

Напомним, что вероятность определенной 2-кратной ошибки определяется формулой: 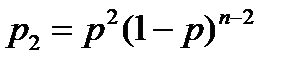. Но таких ошибок может быть несколько. Если, к примеру, кодовое слово состоит из 5 символов, то возможны ошибки в 1 и 5, 1 и 4, 1 и 3, 1 и 2, 2 и 5, 2 и 4, 2 и 3, 3 и 5, 3 и 4, 4 и 5 разрядах. Итого 10 различных 2-кратных ошибок. Их число равно числу сочетаний из 5 элементов по 2.

Если говорить не о конкретных, а о произвольных ко-кратных ошибках, то вероятность 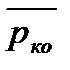их возникновения находится как сумма всех возможных i-кратных конкретных ошибок:

,

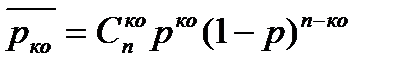где 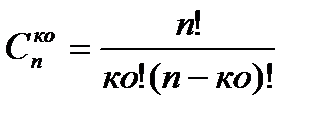− число сочетаний из n элементов по ко.

Следует заметить, что 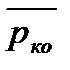в отличие от Р_ко не обязательно монотонно уменьшается с ростом n.

При получении искаженного кодового слова мы имеем дело с конкретной ко-кратной ошибкой, вероятность появления которой − Р_ко . Эта вероятность монотонно уменьшается с ростом кратности ошибки ко. Поэтому при обнаружении на выходе канала запрещенного кодового слова наиболее вероятным является то, что было передано разрешенное кодовое слово, отличающееся от полученного в наименьшем числе разрядов, т.е. находящееся от него на ближайшем расстоянии.

Если код имеет кодовое расстояние d_min , то гарантией обнаружения ошибки будет ко<d_min. В этом случае помехи не смогут преобразовать одно разрешенное кодовое слово в другое разрешенное, поскольку расстояние до ближайшего разрешенного слова равно d_min.

Если кратность ошибки превысит кодовое расстояние, она также может быть обнаружена, но не всегда.

Гарантией же правильного исправления ошибки будет условие ко<d_min/2, так как согласно свойству вероятности ошибки наиболее вероятны ошибки с меньшей кратностью и, следовательно, исправление будет производиться в сторону ближайшего разрешенного кодового слова (рис. 3.8).

Рис. 3.8. Кодовое расстояние.

Для того, чтобы это исправление было верным, необходимо выполнение условия ко<d_min/2.

В связи с этим введено понятие корректирующей способности кода.

Под корректирующей способностью кода понимается максимальная кратность исправляемой с применением этого кода ошибки.

Учитывая вышеприведенные рассуждения, корректирующую способность кода KCK можно было бы определить по формуле:

.

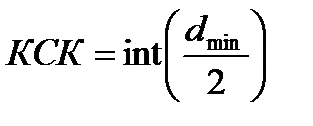На практике же, учитывая увеличение вероятности ошибочного исправления ошибки с ростом ее кратности, реальную корректирующую способность уменьшают:

.

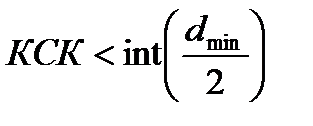В наших рассуждениях мы предполагали использование ДСМК. Если же реальный канал этой модели не соответствует, способы обнаружения и коррекции ошибок видоизменяются.

В общем же процедура обнаружения-исправления ошибок опирается на разбиение всего множества 2ⁿ возможных кодовых комбинаций на 2^k подмножеств, каждое из которых состоит из одного разрешенного кодового слова и соответствующих ему запрещенных. Эти подмножества не пересекаются между собой, а их объединение не обязательно равно исходному множеству.

При приеме определяется, к какому подмножеству относится принятое кодовое слово и, если оно (кодовое слово) не является разрешенным, оно заменяется закрепленным за этим подмножеством разрешенным кодовым словом.

Если же принятое кодовое слово не принадлежит ни одному из подмножеств, фиксируется неисправимое искажение, за чем могут следовать какие-либо дополнительные меры, например, запрос на повторную передачу искаженной части сообщения.

Граница Хэмминга

Граница Хэмминга Q, определяет максимально возможное количество разрешенных кодовых слов равномерного кода при заданных длине n кодового слова и корректирующей способности кода КСК.

Найдем связь между максимально возможной корректирующей способностью КСК, длиной n кодового слова и максимальным числом Q разрешенных кодовых слов в случае использования ДСК.

В круг (шар) диаметром КСК поместится 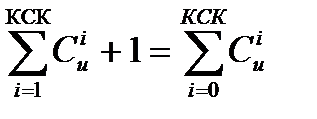кодовых слов.

Поскольку подмножества не пересекаются, то

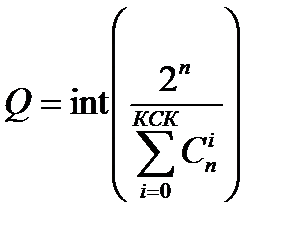. (3.1)

Коды, число кодовых слов которых равно Q, называются оптимальными или плотноупакованными.

В геометрической интерпретации это означает, что круги на плоскости или шары в объеме соприкасаются, не пересекаясь друг с другом, и любая кодовая комбинация обязательно входит в какой-либо круг или шар. Избыточность при этом используется максимально. Однако, если учесть сложность аппаратной или программной реализации, использование оптимальных кодов не всегда выгодно.