I. Теоретическое введение

В электрических цепях вынужденные колебания происходят под действием источника переменного тока (рис.1), Пусть ЭДС источника меняется по гармоническому закону:

ε=ε₀ sin ωt (1)

Запишем для данной цепи второй закон Кирхгоффа:

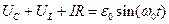(2)

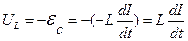где: ; (3)

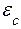- ЭДС самоиндукции катушки,

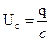(4)

Подставив (3) и (4) в (2) и учтем, что 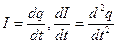, получим:

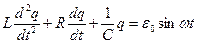(5)

Разделим (5) на L:

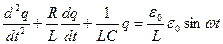(6)

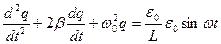или , (7)

где 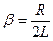- коэффициент затухания,

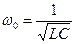- собственная частота колебательного контура.

Выражение (7) называется дифференциальным уравнением вынужденных колебаний.

Решением уравнения (7) будет q=q₀sin(ω₀t+φ) то есть в цепи идет переменный ток частоты, равной частоте генератора.

Рассмотрим цепь с резистором(рис. 2,а), имеющим только омиче­ское сопротивление R. К зажимам ab приложено переменное напряжение:

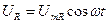(8)

где U_mR — амплитудное значение напряжения,

ω — циклическая частота колебаний.

Используя закон Ома, получим выражение для силы тока:

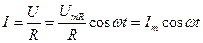(9)

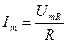где (10)

— амплитуда силы тока.

Как видно из (8) и (9), сила тока и напряжение изменяются в од­ной фазе, что можно представить в виде векторной диаграммы (рис. 2, б). На диаграмме амплитуды U_mR и I_m представлены как одина­ково направленные векторы, равномерно вращающиеся против часовой стрелки с угловой скоростью ω. Проекция этих векторов на «ось токов» (го­ризонтальная прямая) дает мгновенные значения напряжения и силы тока.

Рассмотрим цепь с катушкой индуктивности (рис. 3, а), индуктив­ность которой L, омическое сопротивление равно нулю. Напряжение на зажимах ab цепи, как и в предыдущем случае, выражается зависимо­стью, аналогичной (8):

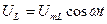(11)

Запишем второй закон Кирхгоффа для данной цепи

.

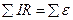Так как активное сопротивление R=0, то 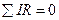. Сумма ЭДС представляет собой ЭДС источника тока, изменяющееся по закону (11) и ЭДС самоиндукции: .

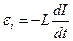Таким образом, получаем

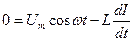(12)

Из (12) следует, что

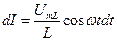
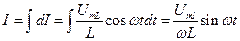(13)

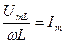где (14)

- амплитуда силы тока.

Так как 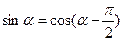, то с учетом (14) формула (13) примет вид

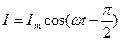(15)

Как видно из (11) и (15), фаза силы тока 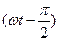,а фаза напря­жения ωt. Следовательно, ток отстает по фазе от напряжения на 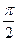, что показано с помощью векторной диаграммы на рис. 3, б.

Сравнивая (14) с законом Ома для участка цепи постоянного тока, заметим, что выражение

X_L = ωL (16)

играет роль сопротивления цепи, которое называют индуктивным. Это сопротивление вместе с U_mL определяет амплитуду силы тока.

Если в цепи имеется только индуктивное сопротивление, то количест­во теплоты в ней не выделяется, так как R = 0. Роль катушки индуктив­ности сводится к накоплению энергии магнитного поля и возвращению этой энергии обратно источнику тока. Таким образом, происходит пери­одическая перекачка энергии от источника в цепь и от цепи к источни­ку, в идеальном случае без потери энергии.

Рассмотрим цепь с конденсаторомэлектроемкостью С (рис. 4, а), омическое сопротивление которого бесконечно велико. Напряжение на зажимах аb цепи выражается зависимостью, аналогичной (8):

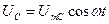(17)

Сила тока в цепи определяется скоростью изменения заряда на об­кладках конденсатора. Используя соотношение для электроемкости ( 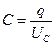), находим

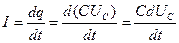(18)

подставив (17) в (18) получим

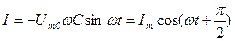, (19)

где 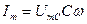. (20)

Как видно из (17) и (19), фаза силы тока 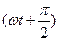,а фаза напря­жения ωt. Следовательно, ток опережает по фазе напряжение на 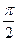, что показано с помощью векторной диаграммы на рис. 4, б.

Сравнивая (20) с законом Ома для участка цепи постоянного тока, заметим, что выражение

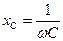(21)

играет роль сопротивления цепи, которое называют емкостным.

В данном случае количество теплоты в цепи не выделяется, так как сопротивление проводников равно нулю. Нагревание диэлектрика в пе­ременном электрическом поле здесь не учитывается. Роль конденсатора сводится к накоплению энергии электрического поля и возвращению этой энергии обратно источнику тока. Происходит периодическая пере­качка энергии от источника в цепь и от цепи к источнику, в идеальном случае без потери энергии.

Рассмотрим цепь, в которой последовательно соединены резистор, катушка индуктивности и конденсатор (рис. 5, а). Напряжение на за­жимах аb цепи, создаваемое внешним источником, как и в предыдущих примерах, изменяется по гармоническому закону с амплитудой U_m:

U = U_m cos ωt (22)

Сумма напряжений на отдельных участках равна внешнему напряжению, а сила тока во всей цепи одинакова, так как соединение последовательное.

Изобразим векторную диаграмму для такой цепи (рис. 5, б). Для этого амплитуды на­пряжений на участках отложим относительно вектора I_m: вектор U_mR — в одной фазе с силой тока; вектор U_mL — с опережением силы тока по фазе на 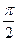, вектор U_mC — с отставанием от силы тока по фазе на .

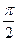Суммируя три вектора, исполь­зуя теорему Пифагора, находим графически значение U_m:

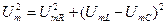. (23)

Подставляя в (23) выражения этих амплитуд из (10), (14) и (20) получим

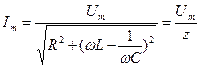(24)

где 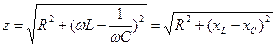— полное сопротивление цепи переменного тока, называемое им­педансом.

Выражение (24) называется законом Ома для цепи переменного тока.

Если индуктивное и емкостное сопротивления цепи при их последова­тельном соединении будут одинаковы (X_L = Х_с), то полное сопротивление цепи имеет наименьшее значение (z = R), а сила тока достигает наибольшего значения.

Такой случай вынужденных электрических колебаний называют резонансом напряжений. Индуктивное и емкостное напряжение при резонансе равны между собой и противоположны по фазе.

Из формул (16) и (21) можно получить выражение для резонансной частоты:

,

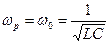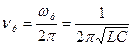(25)

Период колебаний 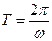, следовательно

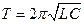(26)

добротность контура Q – это число, показывающее, во сколько раз напряжение U_Lmах или U_Сmах превышает приложенную ЭДС.

При больших добротностях Q резонансные U_Lmах и U_Cmax значительно превышают ЭДС и это используется для усиления слабого сигнала в радиоприемниках. Зависимость тока в цепи от частоты приложенной ЭДС обычно изображают резонансной кривой I=f(ω) или I=f(ν), которая тем "острее", чем меньше R цепи и больше добротность Q (рис.6,а).

Добротность контура может быть рассчитана по графику (рис. 6, б):

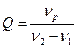(27)

где ν₁ и ν₂ - частоты, при которых ток 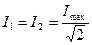. Это значение тока называют действующим значением переменного тока. Аналогично определяется действующее значение напряжения: 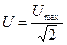. Именно эти значения и показывают приборы в цепи, в отличие от мгновенных значений тока, ЭДС и напряжений, которые непрерывно меняются.

Острота резонансной кривой характеризуется ее относительной полушириной

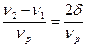(28)

где (ν₂ – ν₁) разность значений частот соответствующих действующему значению тока: ,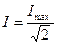

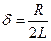(29)

- коэффициент затухания контура.

Из формул (27), (28) и (29) следует, что

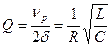(30)