Элементы теории кодирования
Некоторые общие свойства кодов[8].
Рассмотрим на примерах. Предположим, что дискретный источник без памяти, т.е. дающий независимые сообщения – буквы – на выходе, имеет алфавит из k букв, поступающих с вероятностями p1, p2, …, pk.
Каждая буква кодируется с использованием вторичного алфавита из m букв. Обозначим ni – число букв в кодовом слове, которое соответствует i-й букве источника. Нас будет интересовать средняя длина кодового слова nср, которая находится по известной формуле:
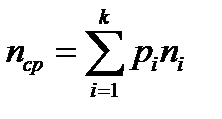 .
.
В качестве примера рассмотрим возможные способы составления кодовых слов двоичного кода при объеме первичного алфавита k=4 (таблица 3.1).
Таблица 3.1.
| i (номер буквы первичного алфавита) | pi | Код 1 | Код 2 | Код 3 | Код 4 |
| 0,5 | |||||
| 0,25 | |||||
| 0,125 | |||||
| 0,125 |
Заметим, что код 1 имеет неудачное свойство, состоящее в том, что буквы с номерами 1 и 2 кодируются одинаково – кодовым словом 0. Поэтому однозначное декодирование при использовании этого кода невозможно.
Код 2 обладает подобным же недостатком: последовательность 11 будет закодирована в 00, что совпадает с кодовым словом для буквы 3. Затруднений для декодирования в этом случае не будет только тогда, когда между кодовыми словами будет добавлен какой-либо разделительный символ. Но если такой символ ввести, то его можно понимать как дополнительную букву вторичного алфавита. Тогда каждое кодовое слово в конце или в начале просто дополняется этой буквой. В результате такой код можно рассматривать как частный случай кодов без разделительных символов. По этой причине коды с разделительными символами отдельно не рассматриваются.
Примером такого кода может служить код 4, где 0 можно понимать как разделительный символ.
Из вышесказанного следует, что код является однозначно декодируемым, если кодовые слова, соответствующие различным буквам первичного алфавита, различны. Это необходимое условие однозначной декодируемости, однако не всегда достаточное.
С точки зрения теории и практики наиболее важными среди всех однозначно декодируемых кодов являются так называемые префиксные коды.
Префиксными называют коды, в которых каждое кодовое слово не является начальной частью (префиксом) другого кодового слова. Это уже достаточное условие однозначной декодируемости.
Нетрудно заметить, что коды 1 и 2 не являются префиксными.
Вопросы студентам:
1) являются ли коды 3 и 4 префиксными?
2) являются ли коды 3 и 4 однозначно декодируемыми?
Коды удобно описывать графически с помощью графа, называемого кодовымдеревом. Это дерево строится из одной вершины и имеет узлы нулевого, первого, второго и т.д. порядков. Из каждого узла выходит m лучей – рёбер, каждому из которых соответствует определенная буква вторичного алфавита.
На рис. 3.2. изображено кодовое дерево кода 3, описанного в таблице 3.1.
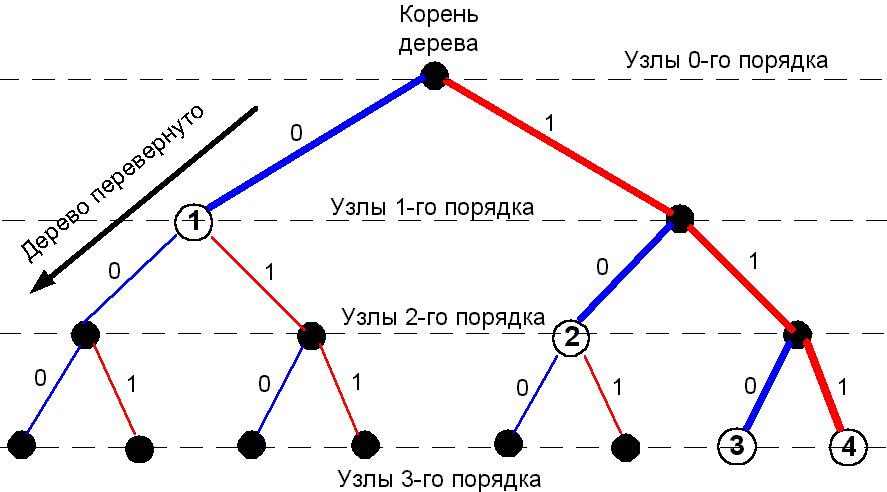
Рис. 3.2. Пример кодового дерева двоичного кода.
Каждому i-му кодовому слову длиной ni ставится в соответствие узел xi i-го порядка и определенный путь по кодовому дереву от корня до этого узла.
Из графического представления следует, что код будет префиксным, если узлы, соответствующие кодовым словам, являются концевыми, т.е. через них не лежит путь к другим узлам, также соответствующим кодовым словам.
Заметим, что из каждого узла кодового дерева выходит m ребер и доля всех узлов любого порядка выше 0-го, приходящегося на один узел 1-го порядка равна 1/m=m-1.Далее, через 1 узел второго порядка проходят пути к 1/m2=m-2 части всех узлов любого из узлов более высокого порядка и т.д. В общем случае через 1 узел i-го порядка проходят пути к m-i части узлов любого из узлов более высокого порядка.
Учитывая последнее, докажем теорему, известную как Неравенство Крафта
Неравенство Крафта
Теорема 1. Если целые числа n1, n2, …, nk удовлетворяют неравенству
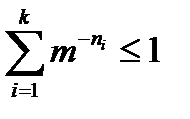 , (3.1)
, (3.1)
существует префиксный код с алфавитом объемом m, длины кодовых слов которого равны этим числам. И обратно, длины кодовых слов любого префиксного кода отвечают неравенству Крафта (3.1).
Доказательство
Предположим, что неравенство Крафта 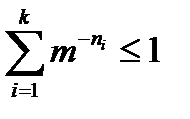 выполняется. Построим соответствующий префиксный код (первая часть теоремы).
выполняется. Построим соответствующий префиксный код (первая часть теоремы).
Упорядочим длины ni в порядке возрастания ( 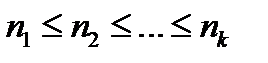 ).
).
Выберем какой-либо узел x1 порядка n1 в полном кодовом дереве в качестве концевого. Это запретит использование  части узлов n1-го и более высокого порядка для выбора в качестве концевых для других кодовых слов.
части узлов n1-го и более высокого порядка для выбора в качестве концевых для других кодовых слов.
Среди тех узлов, которые еще можно использовать в качестве концевых, выберем узел x2 порядка n2 в качестве концевого. Это запретит использование еще  части узлов n2-го и более высокого порядка для выбора в качестве концевых для других кодовых слов и т.д.
части узлов n2-го и более высокого порядка для выбора в качестве концевых для других кодовых слов и т.д.
Сумма 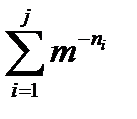 на j-м этапе <1 и это значит, что для следующего i+1-го кодового слова еще есть возможность выбора узла.
на j-м этапе <1 и это значит, что для следующего i+1-го кодового слова еще есть возможность выбора узла.
Запрещенные к использованию узлы не пересекаются. Следовательно, общая доля запрещенных узлов равна сумме долей, запрещенных к использованию уже выбранными концевыми узлами. Эта доля равна 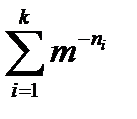 по предположению
по предположению 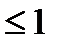 . А это означает, что остались некоторые узлы более высокого порядка, разрешенные к использованию в качестве концевых.
. А это означает, что остались некоторые узлы более высокого порядка, разрешенные к использованию в качестве концевых.
Для этого мы расположили n в порядке возрастания. Для пояснения нужно обратиться к кодовому дереву (рис.3.2).
Для доказательства второй части теоремы о том, что длины любого префиксного кода отвечают неравенству Крафта (3.1), заметим, что префиксному коду соответствует определенный набор концевых узлов, каждый из которых закрывает 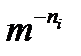 долю узлов того же и более высокого порядка для использования в качестве концевых. Эти доли не пересекаются, следовательно, их сумма не может превышать 1. Отсюда
долю узлов того же и более высокого порядка для использования в качестве концевых. Эти доли не пересекаются, следовательно, их сумма не может превышать 1. Отсюда 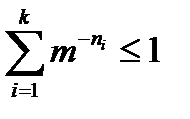 , что и требовалось доказать.
, что и требовалось доказать.
Дата добавления: 2021-04-21; просмотров: 616;











