Теорема об обобщении некоторых результатов, полученных для префиксных кодов, на все однозначно декодируемые коды

Докажем теперь теорему, позволяющую обобщать некоторые результаты, полученные для префиксных кодов на все однозначно декодируемые коды.

Теорема 2.

Формулировка. Пусть задан код с длинами кодовых слов n₁, n₂, … , n_k и с алфавитом объема m. Если код однозначно декодируем, неравенство Крафта 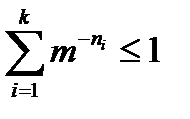удовлетворяется.

Доказательство.

Пусть z – произвольное положительное число.

Рассмотрим тождество:

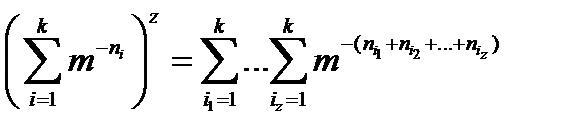. (3.2)

Заметим, что 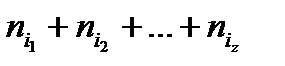можно понимать как сумму длин z кодовых слов. Обозначим эту сумму через j (j= 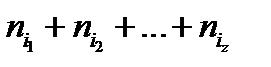), а количество комбинаций, дающих одинаковую сумму длин A_j . Тогда (3.2) можно записать в виде: .

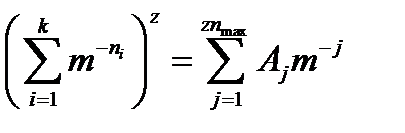Если код однозначно декодируем, то все последовательности кодовых слов с суммарной длиной j кодовых букв (букв вторичного алфавита) являются различными. Поэтому A_j <=m^j , так как m^j – общее число всевозможных комбинаций из m букв по j. Из этого следует:

;

.

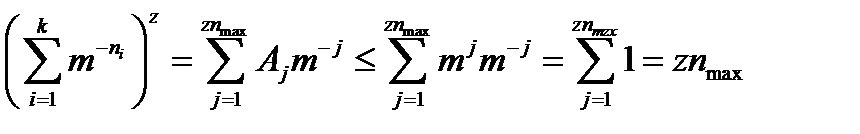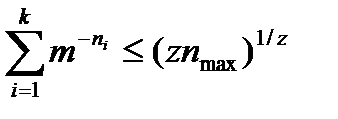Поскольку z – произвольное число, устремим его в бесконечность:

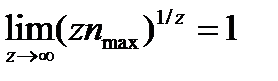, что можно доказать, используя правило Лопиталя.

Отсюда следует, что 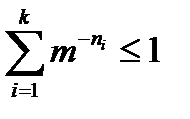− неравенство Крафта.

Согласно теореме 1 существует префиксный код с теми же n₁, n₂, … ,n_k . Поэтому все результаты, полученные для префиксных кодов относительно средней длины кодового слова n_ср , распространяются и на все однозначно декодируемые коды.

Теорема 2 доказана.