Оптимальное квантование по уровню

Рисунком 2.13 иллюстрируется принцип квантования по уровню[7].

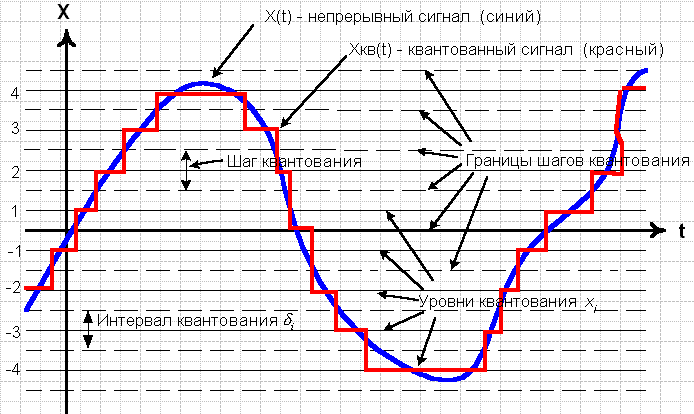
Рис. 2.13. Квантование по уровню.

Это квантование сводится к замене значения исходного сигнала уровнем того шага, в пределы которого оно (это значение) попадает. Как уже говорилось, шкала квантования по уровню характеризуется совокупностью границ интервалов квантования 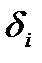и уровней квантования X_i.

Количество передаваемых или хранимых данных о сигнале прямо пропорционально количеству уровней квантования. Следовательно, чем этих уровней меньше, тем меньше число передаваемых или хранимых данных и тем экономичнее система передачи или хранения квантованного сигнала.

Совсем необязательно, что бы шаги квантования по уровню были одинаковыми. Тогда, варьируя параметрами шкалы квантования, можно, к примеру, добиться минимально возможной при заданном числе шагов квантования дисперсии ошибки. Или, наоборот, задавшись дисперсией ошибки, найти параметры шкалы квантования (положение уровней и границ шагов квантования), при которых число уровней квантования минимально.

Вывод нужных соотношений будем вести, предполагая, что число уровней квантования достаточно велико, а скорость изменения квантуемого сигнала настолько мала, чтобы закон распределения ошибки внутри каждого из интервалов квантования можно было считать равномерным.

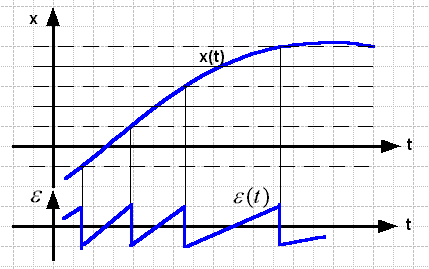Рис. 2.14. График ошибки квантования ε(t).

Это предположение иллюстрируется рис. 2.14.

Из этого следует, что функция ошибки 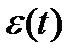имеет пилообразную форму и что, чем меньше размер шага квантования, тем эта форма ближе к идеально пилообразной. А это в свою очередь означает, что вероятности значений ошибки в пределах интервала квантования равны, т.е. закон распределения этих значений является равномерным.

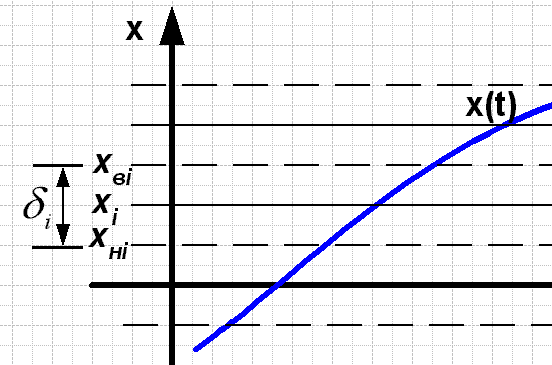Рис. 2.15. Обозначения.

Зададимся целью найти такую шкалу квантования по уровню, при которой среднее значение квадрата ошибки минимально.

Введем обозначения (рис. 2.15):

x_нi – нижняя граница шага квантования;

x_вi – верхняя граница шага квантования;

x_i – уровень квантования;

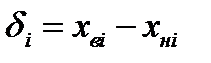- размер i-го шага квантования.

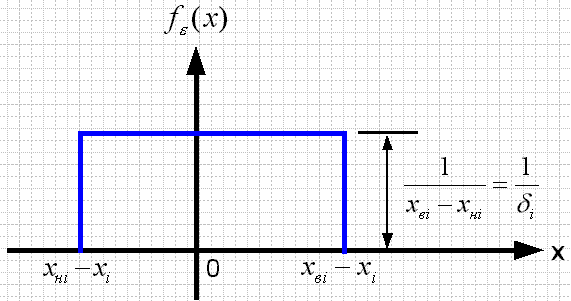Рис. 2.16. Закон распределения ошибки.

Тогда ошибка 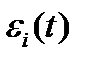на i-м интервале распределена по равномерному закону (см. рис. 2.16).

Выведем для этого случая формулы математического ожидания 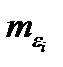и дисперсии 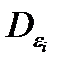ошибки квантования на i-м интервале.

,

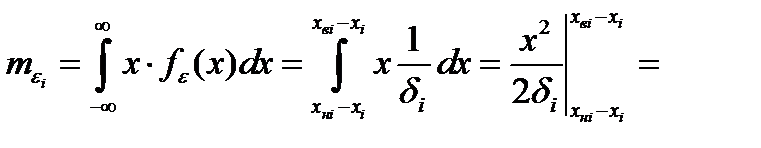
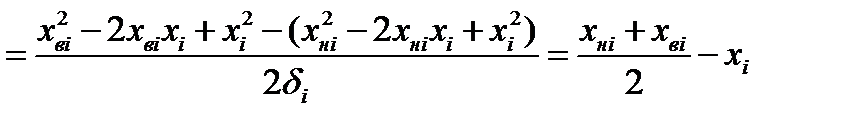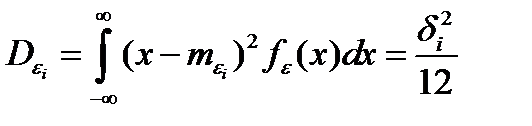
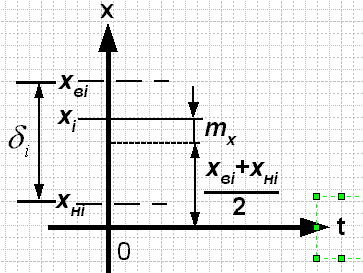Рис. 2.17. Обозначения.

(источник − справочные данные для равномерного закона распределения).

Среднее значение квадрата ошибки на i-м уровне квантования по определению находится по формуле:

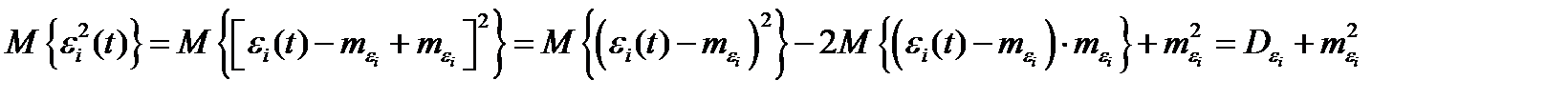, так как .

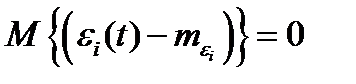Дисперсия 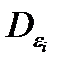от положения уровня квантования x_i не зависит, а

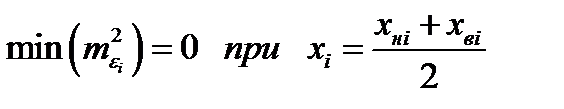
(см. формулу )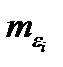

Следовательно, для минимизации среднего значения квадрата ошибки уровни квантования должны помещаться в центре соответствующих шагов квантования.

При этом не надо забывать о предположении достаточно большого числа уровней квантования, из-за чего стало возможным предположение о равномерном законе распределения ошибки.

Доказано, что значения функции ошибки 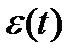при различных i можно считать независимыми. Поэтому среднее значение квадрата ошибки по всем уровням 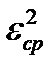можно выполнить по известной формуле:

,

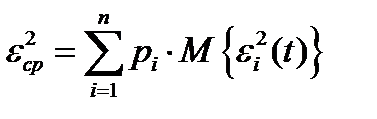где p_i – вероятность попадания квантуемого сигнала в i-й интервал квантования,

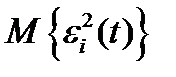− среднее значение квадрата ошибки на i-м интервале квантования.

Так как p_i от положения уровня квантования x_i внутри интервала квантования не зависит, то минимизация среднего значения квадрата ошибки на каждом из уровней приведет к минимизации среднего значения квадрата ошибки вообще.

При 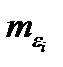=0 среднее значение квадрата ошибки 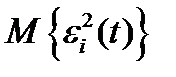= 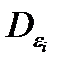, поэтому

.

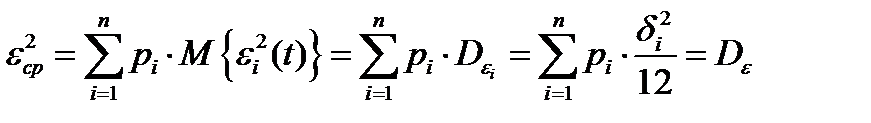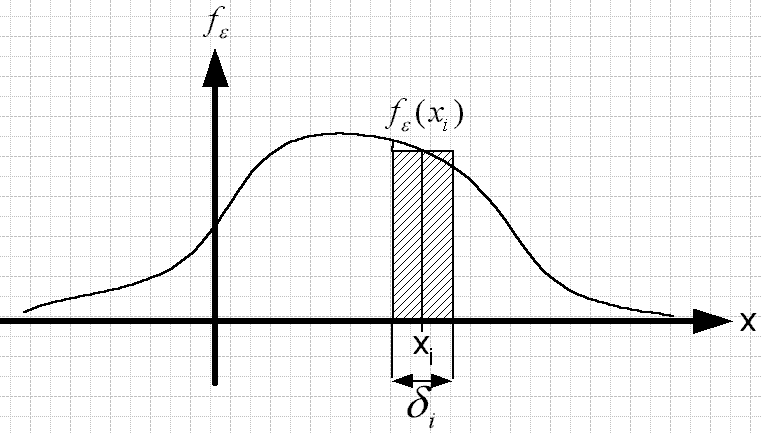Рис. 2.18. К расчету вероятности попадания значения сигнала в пределы шага.

При малых шагах 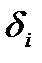можно считать 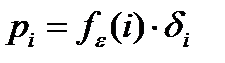(рис. 2.18).

Тогда

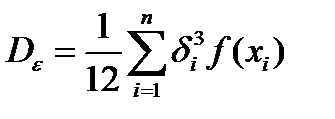(2.20)