Великой теоремы Ферма

Уже доказательство Великой теоремы Ферма для показателя n = 3 не элементарно. Впервые полученное Эйлером, оно в течение многих лет оставалось идейным источником для дальнейших обобщений и модификаций.

Идея проста: если x³ + y³ = z³ для целых x, y, z, не равных нулю, то

z³ = (x + y)×(x² – x×y + y²) = (x + y)×(x – w×y)×(x + w²×y),

где w = 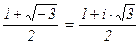, w² = 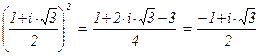= w – 1 , а w³ = –1. Таким образом, z³ разложено в произведение трёх множителей из множества чисел K = {z = p + w×q Î C | p, q Î Z }. Легко проверить, что это множество замкнуто относительно сложения, вычитания и умножения:

(p + w×q) ± (r + w×s) = (p ± r) + w×(q ± s) Î K ,

(p + w×q)×(r + w×s) = p×r + w×(q×r + p×s) + w²×q×s =

= p×r + w×(q×r + p×s) + (w – 1)×q×s = (p×r – q×s) + w×(q×r + p×s + q×s)Î K .

Такие подмножества в C называют числовыми кольцами. В них можно производить вычисления почти как с целыми числами.

Как известно, любое целое число единственным образом раскладывается в произведение простых: z = 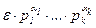, где e Î {–1, +1}, p_i – простые числа, a_i Î N (1 £ i £ k). Отсюда следует, что если произведение нескольких попарно взаимно простых целых чисел является m-й степенью некоторого целого числа, то каждый из сомножителей (с точностью до знака) является m-й степенью целого числа. Действительно, если t^m = u₁×…×u_k , то имеет место разложение в натуральных числах: |t|^m = |u₁|×…×|u_k|, где сомножители попарно взаимно просты: НОД(|u_i|, |u_j|) = 1. Это значит, что в канонических разложениях чисел |u₁|, … , |u_k| нет одинаковых простых чисел, а показатель степени каждого простого числа делится на m, т.к. этот показатель является показателем степени этого же простого числа в |t|^m. Итак, |u_i| = v_i^m (1 £ i £ k) и |t| = v₁× … ×v_k для некоторых натуральных чисел v₁ , … , v_k .

Если предположить, что аналогичный факт имеет место для числового кольца K, то Великая теорема Ферма доказывается просто. Из разложения z³ = (x + y)×(x + w×y)×(x – w²×y) и попарной взаимной простоты целых чисел x, y, z следует, что взаимно просты и множители в этом разложении. Действительно, если, например x + w×y, x – w²×y делятся на некоторое простое в K число π = p + w×q, то

x + w×x = (1 + w)×x = (x + w×y)×w + (x – w²×y) M π ,

–y + 2×w×y = (2×w – 1)×y = w×(1 + w)×y = (x + w×y) – (x – w²×y) M π ,

что невозможно: если x + w×x = (p +w×q)×(k + w×l), y = (p +w×q)×(m + w×n).