Выбор экономичного режима совместной работы конденсационных электростанций при использовании топлива одинакового качества и цены
Рассмотрим энергосистему, состоящую из n конденсационных электростанций, работающих на топливе одинакового качества и цены и покрывающих постоянную нагрузку системы Pс. Известны энергетические характеристики выбранного состава работающего оборудования для каждой i-й станции вида 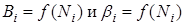 .
.
Задача оптимизации режима совместной работы n электростанций формулируется следующим образом – минимизировать расход топлива по системе
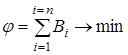 (7.9)
(7.9)
при условии соблюдения баланса мощности системы в каждый момент времени t
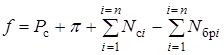 , (7.10)
, (7.10)
где Вi — часовой расход топлива i-й станцией; Nбрi – активная мощность брутто i-й станции; p — потери активной мощности в сетях системы; Nсi– расход мощности на собственные нужды i-й станции.
Задача выбора экономичного режима сводится, как было показано выше, к нахождению условного минимума функции Лагранжа
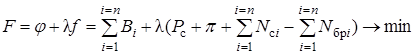 . (7.11)
. (7.11)
Выражение для первых производных функции Лагранжа получает для i-й станции следующей вид:
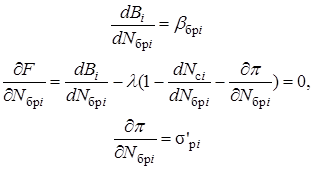 (7.12)
(7.12)
где bбрi – частичный удельный расход брутто i-той станции; sэi – частичная удельная потеря мощности на собственные нужды i-той станции; s'рi- частичная удельная потеря распределения энергии в сетях по нагрузке брутто i-той станции, причем
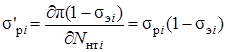 , (7.13)
, (7.13)
где sрi – частичная удельная потеря распределения энергии в сетях по нагрузке нетто i-той станции.
Используя эти обозначения, получим условие достижения минимума функции (7.11) ,и, следовательно, функции (7.9) при условии (7.10)
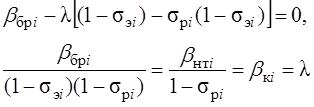
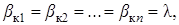 (7.14)
(7.14)
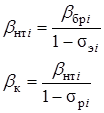
где bнтi – частичный удельный расход нетто i-той станции; bк – конечный частичный удельный расход i-той станции, учитывающий потери энергии в сетях.
Таким образом, условие экономичности совместной работы электростанций в системе сводится к их работе с такими мощностями, при которых конечные частичные удельные расходы равны постоянной величине l, зависящей от величины нагрузки системы 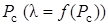 .
.
Для практической реализации условия (7.14) могут использоваться два метода выбора экономичного режима: графический и табличный.
Графический метод применим при небольшом числе электростанций. Используя зависимости bкi = f (Nбрi ) строят энергетическую характеристику системы bк c = f(Ne ). Затем, исходя из условия равенства bкi = bк c = l можно получить нагрузку каждой станции при любой нагрузке системы Рct (рис. 7.2).
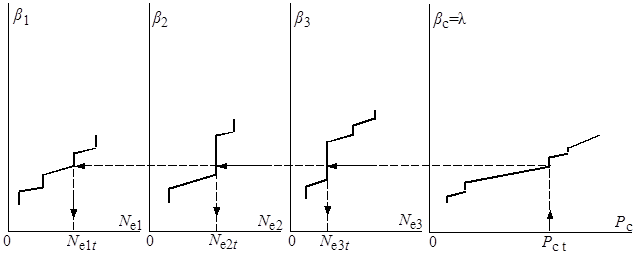 Рис. 7.2. Графический метод выбора экономичного распределения суммарной нагрузки системы между конденсационными электростанциями, использующими топливо одинакового качества и цены
Рис. 7.2. Графический метод выбора экономичного распределения суммарной нагрузки системы между конденсационными электростанциями, использующими топливо одинакового качества и цены
Табличный метод заключается в построении так называемых диспетчерских таблиц. Эти таблицы строятся по возрастающим значениям частичных удельных расходов электростанций (табл. 7.1) и позволяют определить очередность загрузки различных электростанций при изменении нагрузки энергосистемы Рс.
Таблица 7.1
| Частичный удельный расход,тут/МВт·ч | Нагрузка системы, Рс , МВт | Нагрузка электростанций, МВт | |||||
| Nбр1 | Nбр2 | Nбр3 | Nбр4 | Nбр5 | Nбр6 | ||
| 0,30 | |||||||
| 0,32 | |||||||
| 0,34 | |||||||
| 0,36 | |||||||
| 0,38 | |||||||
| 0,40 | |||||||
| Продолжение табл. 7.1 | |||||||
| Частичный удельный расход,тут/МВт·ч | Нагрузка системы, Рс , МВт | Нагрузка электростанций, МВт | |||||
| Nбр1 | Nбр2 | Nбр3 | Nбр4 | Nбр5 | Nбр6 | ||
| 0,42 | |||||||
| 0,44 | |||||||
| 0,46 | |||||||
| 0,48 |
На практике в связи со значительными трудностями, обусловленными наличием огромного числа агрегатов и электростанций в системе, а также в связи с необходимостью учета большого числа различных факторов, задача оптимизации суточных режимов работы энергосистемы решается с использованием современных методов математического программирования и вычислительной техники.
Задача выбора экономичного режима значительно усложняется, если дополнительно нужно выбрать состав работающего оборудования. При заданной постоянной величине нагрузки Рс = соnst эта проблема может быть решена, если пренебречь влиянием потерь в электрических сетях. При этом отбор лучшего сочетания работающего оборудования для каждой электростанции может быть произведен по величине наименьшего удельного расхода нетто агрегатов, соответствующего их экономической мощности, исходя из баланса мощности системы с учетом необходимого резерва мощности Rрез.
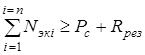 . (7.15)
. (7.15)
Решение задачи выбора экономичного режима работы еще больше усложняется, если нагрузка системы изменяется во времени Рс = f (t). При этом может изменяться и состав включенного оборудования. Практически эту задачу решают следующим образом. Отобрав наиболее экономичную группу оборудования для покрытия максимальной суточной нагрузки Рсмах, при снижении нагрузки решают вопрос о целесообразности отключения одного из агрегатов с учетом дополнительных потерь, связанных с остановкой и последующим пуском агрегата.
Дата добавления: 2020-07-18; просмотров: 661;











