Высокая экономичность представления и точность восстановления исходного сигнала с помощью ряда Котельникова

1) высокую экономичность представления и точность восстановления исходного сигнала с помощью ряда Котельникова;

2) соответствие максимального значения ошибки восстановления расчетному при использовании для восстановления полиномов Лагранжа разных степеней.

В качестве квантуемого непрерывного сигнала берется звук вашего голоса, пропущенный через фильтр, ограничивающий спектр сигнала сверху. Современные операционные системы, в частности Windows, имеют в своем составе средства записи и воспроизведения звука. Необходимо только, чтобы компьютер был оснащен звуковой картой. Индивидуальность голоса обеспечивает различие получаемых результатов.

Для решения первой задачи используется теорема Найквиста-Котельникова, согласно которой для абсолютно точного восстановления непрерывного сигнала по отсчетам, взятым с постоянным шагом 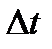, нужно, чтобы этот шаг был взят в соответствии с неравенством: 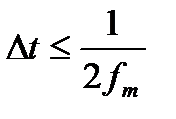, где f_m – частота, выше которой спектр квантуемого сигнала равен 0.

Если шаг дискретизации отвечает этому условию, то согласно теореме Найквиста-Котельникова исходный сигнал x(t) можно восстановить при всех значениях времени (аргумента t) по формуле (ряд Котельникова):

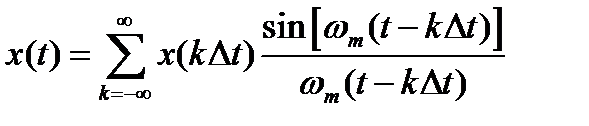(1)

Здесь:

x(t) – исходная дискретизируемая функция;

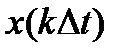- отсчеты функции x(t), взятые в моменты времени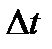

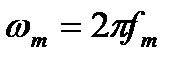- круговая частота.

Проблема, однако, заключается в том, что, как доказано математически, поскольку все реальные сигналы конечны во времени, их спектры не ограничены по частоте. Следовательно, на самом деле для всех реальных сигналов . Поэтому в чистом виде теорему Найквиста-Котельникова применить невозможно. Тем не менее, ее используют, пренебрегая малыми значениями спектра. Это и предлагается сделать в этой работе. Платой за такое пренебрежение будет неточное выполнение равенства (1).

Решение второй задачи основано на использовании формулы максимального значения ошибки (отклонения восстановленного значения функции от исходного):

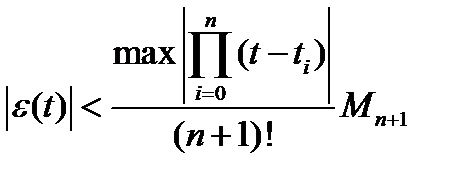(2)

Здесь 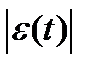- абсолютное значение ошибки;

n – порядок полиномов Лагранжа, используемых для восстановления исходной функции;

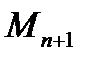- максимальное значение абсолютной величины производной (n+1)–го порядка исходного сигнала x(t);

t – текущее время;

t_i – время взятия i-го отсчета.

Используя эту формулу, задавшись максимально допустимым значением ошибки восстановления исходной функции по периодически взятыми отсчетам, и порядком используемых в воспроизводящей функции полиномов Лагранжа, можно найти максимально возможный шаг квантования (чем шаг квантования больше, тем лучше, поскольку тем меньше приходится брать отсчетов).

В следующей ниже таблице приведены формулы расчета максимального шага дискретизации по времени 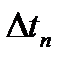в зависимости от порядка n полинома Лагранжа и максимально допустимого значения ошибки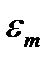

n – порядок используемых для восстановления исходного процесса полиномов Лагранжа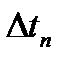

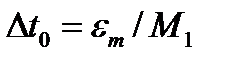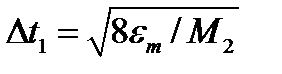Эти формулы и предлагается использовать в данной работе. Их вывод приводится в методическом пособии [1].