Глава 4. Схема независимых испытаний Бернулли. Предельные теоремы в схеме Бернулли
Рассмотрим некоторый стохастический эксперимент, который будем называть испытанием. Среди исходов этого испытания будем различать только два события 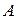 и
и 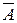 ,
, 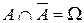 . Если испытание заканчивается появлением события
. Если испытание заканчивается появлением события 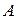 , будем говорить, что наступил «успех», если же испытание заканчивается появлением события
, будем говорить, что наступил «успех», если же испытание заканчивается появлением события 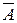 , то говорим, что наступил «неуспех». Обозначим вероятность «успеха»
, то говорим, что наступил «неуспех». Обозначим вероятность «успеха» 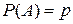 , вероятность «неуспеха»
, вероятность «неуспеха» 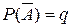 . Очевидно, что
. Очевидно, что 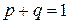 .
.
Теперь рассмотрим эксперимент, состоящий в том, что проводится 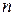 независимых испытаний. Вероятность успеха не изменяется в зависимости от номера испытания.
независимых испытаний. Вероятность успеха не изменяется в зависимости от номера испытания.
Такая схема проведения эксперимента называется схемой независимых испытаний Бернулли.
Рассмотрим случайную величину 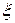 – «количество успехов в
– «количество успехов в 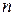 независимых испытаниях Бернулли». Множеством значений этой величины будет множество
независимых испытаниях Бернулли». Множеством значений этой величины будет множество 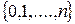 . Обозначим вероятность того, что в
. Обозначим вероятность того, что в 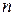 испытаниях появится ровно
испытаниях появится ровно 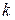 «успехов» как
«успехов» как 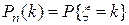 . Имеет место формула Бернулли
. Имеет место формула Бернулли
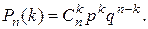 (4.1)
(4.1)
Теорема(Пуассон).
Если последовательность положительных чисел 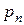 такова, что
такова, что 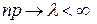 при
при 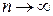 , то
, то 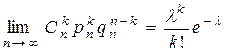 , где
, где 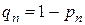 .
.
Из теоремы Пуассона следует, что если 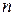 велико и
велико и 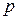 мало, то
мало, то
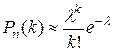 , где
, где 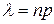 . (4.2)
. (4.2)
Значения 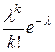 приведены в приложении 3.
приведены в приложении 3.
Дата добавления: 2022-02-05; просмотров: 580;











