Второй случай (заданы дисперсия и математическое ожидание сл. величины)

Предположим теперь, что область определения значений случайной величины не ограничена, но задана ее дисперсия D и математическое ожидание M. Заметим, что дисперсия прямо пропорциональна мощности сигнала.

Из этого следуют следующие условия, накладывающие ограничения на искомый закон распределения:

;

;

.

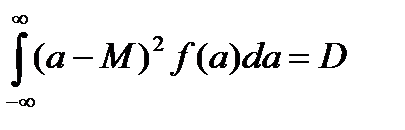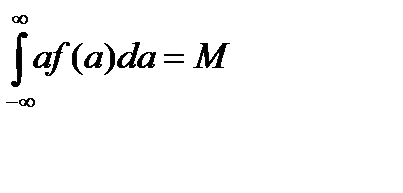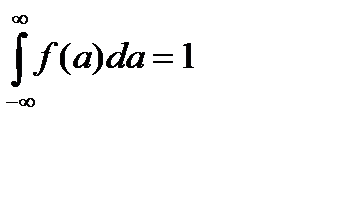Опять будем искать функцию f(a), при которой дифференциальная энтропия принимает максимальное значение. Еще раз используем метод множителей Лагранжа. Вспомогательная функция Ф в этом случае имеет вид:

.

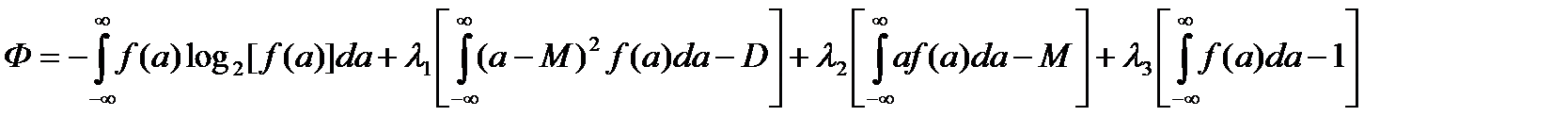Дифференцируя по f(a), получим систему уравнений:

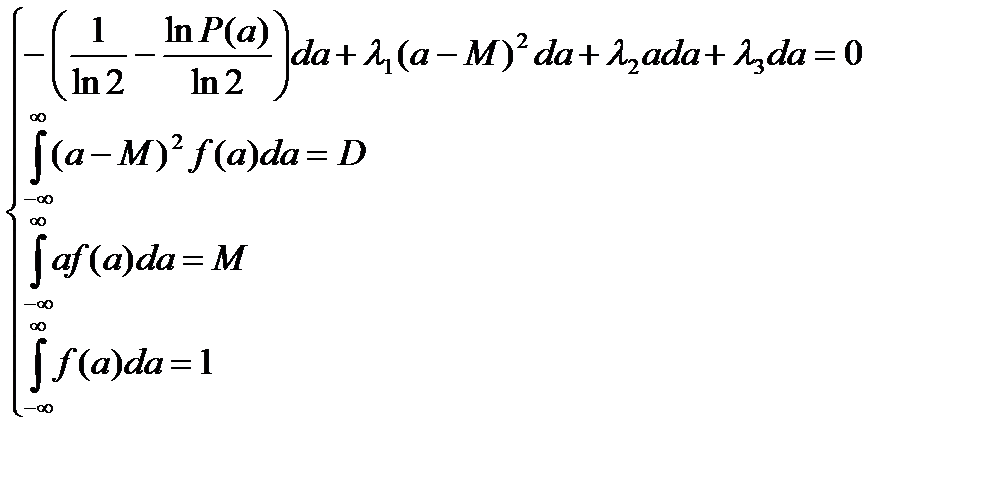
Используя первое уравнение, найдем :

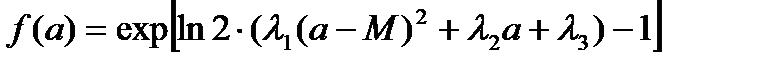(1.2)

Подставим f(a) в 3-е условие:

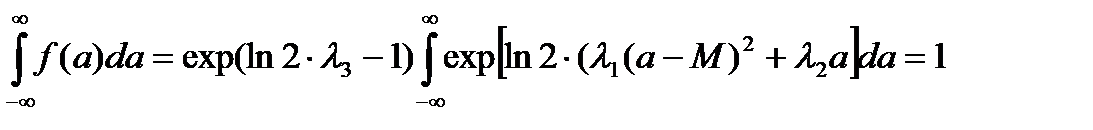(1.3)

По таблицам находим значение интеграла:

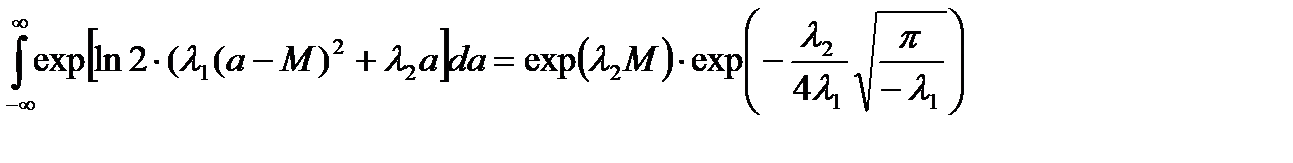(1.4)

Подставив найденный интеграл (1.4) в (1.3), получим:

.

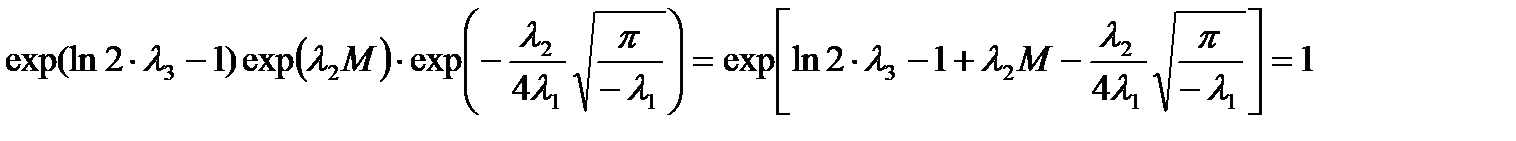Значит 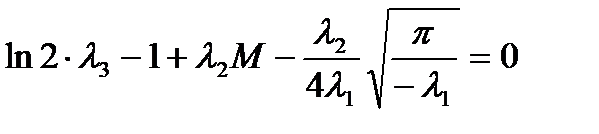и 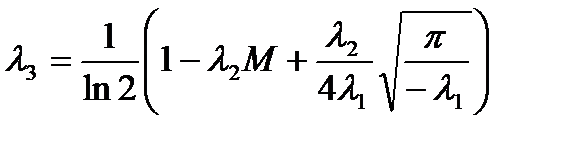. (1.5)

Теперь (1.5) нужно подставить в f(a) (1.2), полученный результат подставить во второе условие и найти λ₂. Далее λ₂ подставляется в f(a) (1.2), а полученный результат – в первое условие. Таким образом, находится λ₁. Далее λ₁ подставляется в f(a) (1.2), в результате чего находится искомый закон распределения: .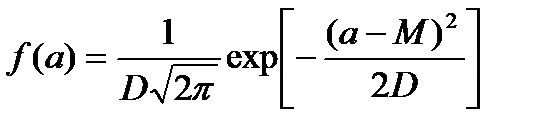

Видим, что это часто встречающийся в природе нормальный закон распределения. Его вид зависит от 2 параметров – математического ожидания (среднего значения) M и дисперсии D, описывающей степень разброса случайной величины.

На рис. 1.6. изображены графики этого закон при разных значениях математического ожидания и дисперсии.

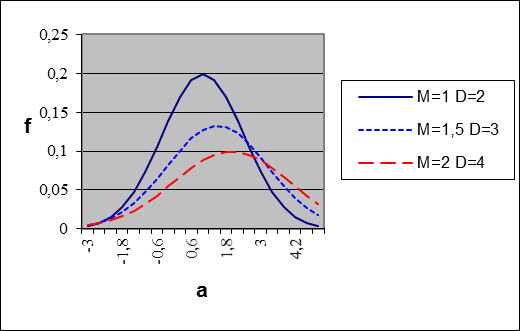
Рис. 1.6. Графики нормального закона распределения