Динамическая энтропия

Здесь энтропия рассматривается как функция времени. При этом преследуется цель – избавиться от неопределенности, т.е. добиться положения, когда энтропия равна 0. Такая ситуация характерна для задач распознавания образов, диагноза болезней, расследования преступлений и т.п.

Количество информации в этом случае рассчитывается как разность энтропии в предыдущий момент времени (до получения новых сведений в результате действий, выполняющихся с целью уменьшения неопределенности) и энтропии в последующий момент времени, т.е. информация характеризует динамику изменения энтропии во времени.

Обычно во всех вышеперечисленных задачах существует 2 набора объектов – возможные причины и возможные следствия. Связи между ними характеризуются набором взаимных или условных вероятностей P_ij(t).

Здесь существует зависимость этих вероятностей от времени. Энтропия 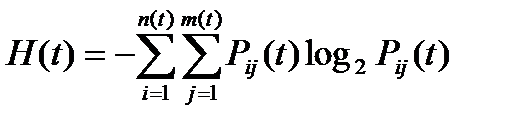, где n(t) и m(t) – меняющиеся количества причин и следствий.

В процессе расследования преступления, действий по распознаванию образов и т.п. изменяются вероятности P_ij, а также количество причин и следствий n(t) и m(t) (рис.1.2).

Рис. 1.2. Изменение энтропии во времени.

Новая энтропия: .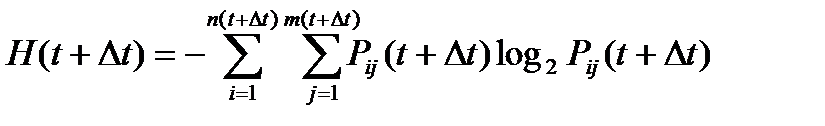

Количество полученной при этом информации: .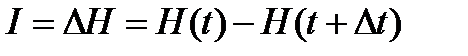

По сути дела определение количества информации через динамическую энтропию не противоречит шенноновскому определению количества информации. Отличие заключается в специфике области применения и в следующих из этого выводах. Шенноновская теория развита с ориентацией на задачи связи при постоянных статистических характеристиках.