Первый случай (значения сл. величины ограничены интервалом)

Случайная величина a ограничена интервалом [b,c]. В этом случае определенный интеграл ее плотности распределения вероятностей (дифференциального закона распределения вероятностей) на этом интервале равен 1: 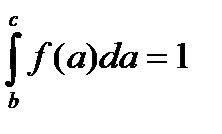. (1.1)

Найдем аналитическое выражение для закона f(a), который дает максимум дифференциальной энтропии

.

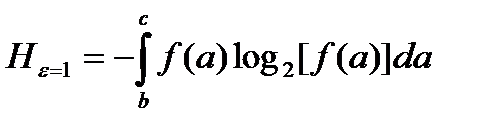Эту задачу можно интерпретировать как предельный случай задачи на поиск условного экстремума функции бесконечного количества аргументов. Эти аргументы – точки искомого плотности распределения вероятностей f(a). А (1.1) является условием, которое нужно соблюсти при поиске экстремума.

Для решения этой задачи воспользуемся вышеописанным методом множителей Лагранжа, который для непрерывного случая переходит в вариационное исчисление.

Вспомогательная функция Ф в нашем случае будет иметь вид:

.

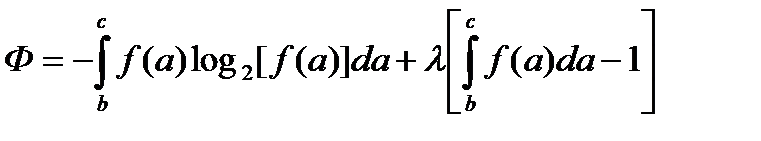Дифференцируя по f(a), получаем систему уравнений:

.

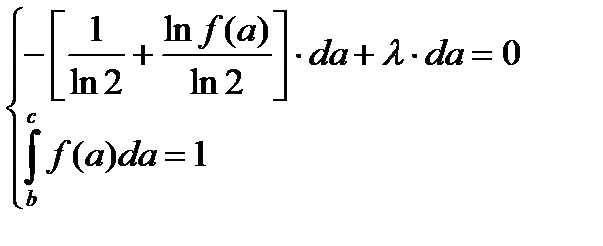Из верхнего уравнения получим .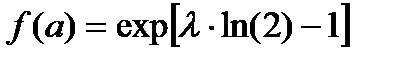

Подставим f(a) в нижнее уравнение, учитывая, что f(a) от а не зависит:

.

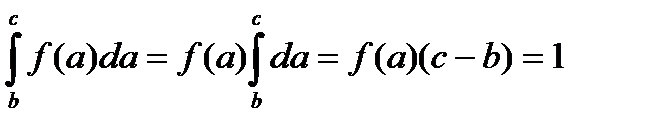Отсюда .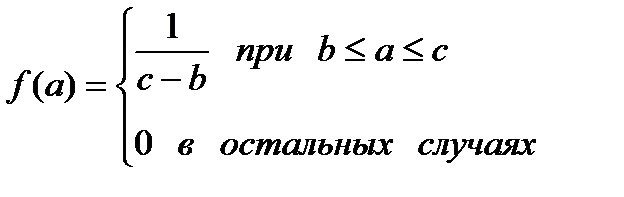

В итоге мы получили уже известный для дискретных сообщений результат, указывающий на то, что максимум энтропии достигается, если все значения сигнала равновероятны, т.е. такой сигнал имеет равномерный закон распределения.