Третий случай (сл. величина принимает только положительные значения)
Аналогичным образом можно показать, что если случайная величина может принимать только положительные значения, т.е. 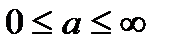 , то максимальная дифференциальная энтропия получается при распределению сигнала по экспоненциальному закону:
, то максимальная дифференциальная энтропия получается при распределению сигнала по экспоненциальному закону:
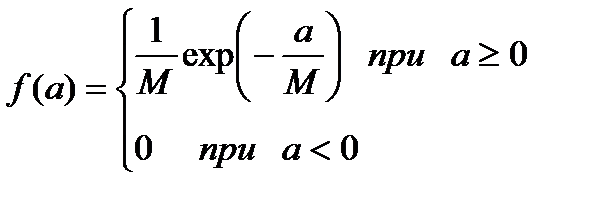 , где M – математическое ожидание.
, где M – математическое ожидание.
Ни рис. 1.7. изображены графики экспоненциального закона распределения при М=1 и М=2.
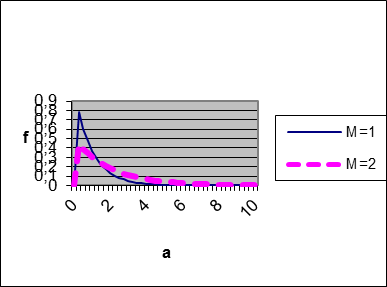
Рис. 1.7. Графики экспоненциального закона распределения.
1.5.2. Информативность (ε-энтропия) случайных величин, распределенных по некоторым наиболее известным законам распределения
Нормальный закон распределения
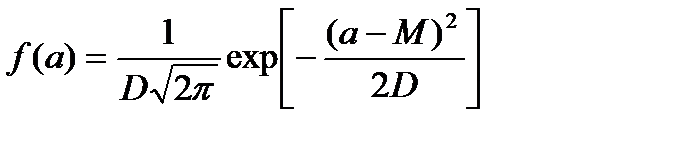 ;
;
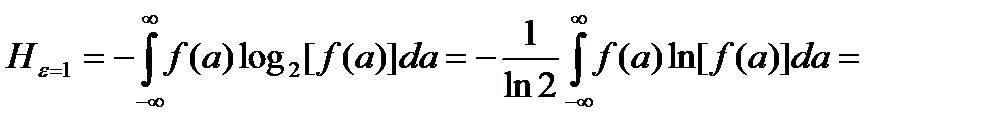
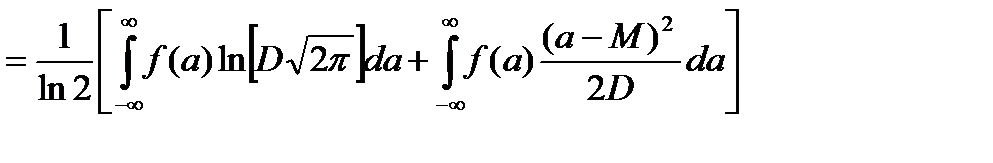 . (1.6)
. (1.6)
Учтем, что константа 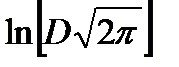 может быть вынесена из под знака интеграла в первом слагаемом (1.6), а сам интеграл в этом случае равен 1.
может быть вынесена из под знака интеграла в первом слагаемом (1.6), а сам интеграл в этом случае равен 1.
Константу  можно вынести из-под знака второго интеграла (5), а сам интеграл представляет собой дисперсию D.
можно вынести из-под знака второго интеграла (5), а сам интеграл представляет собой дисперсию D.
Учитывая все это, получаем:
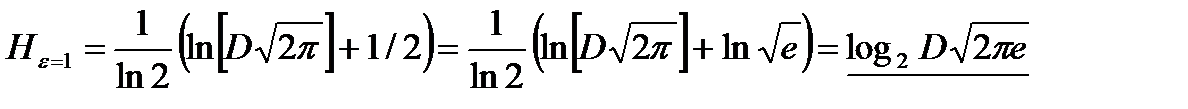 .
.
Равномерный закон распределения.
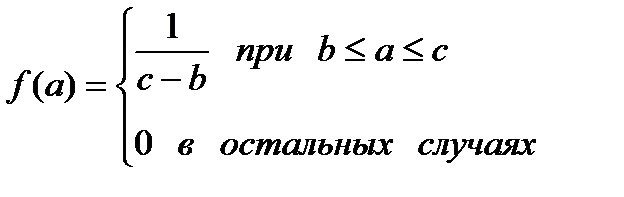 ;
;
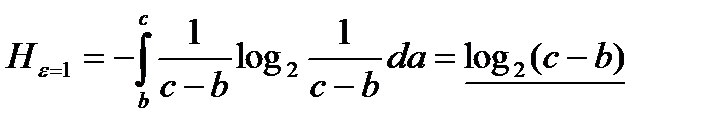 .
.
Экспоненциальный закон распределения
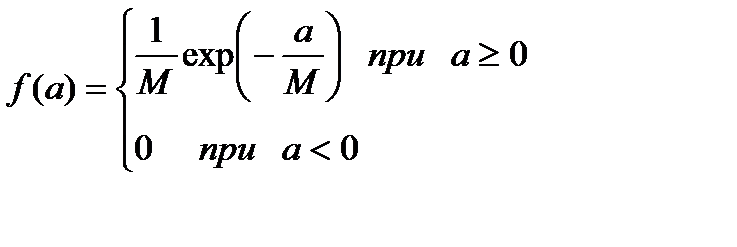 ;
;
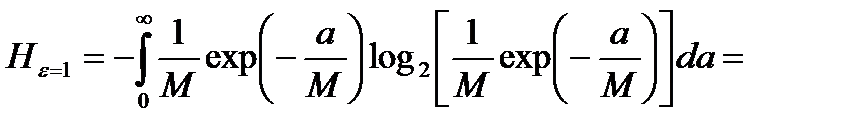
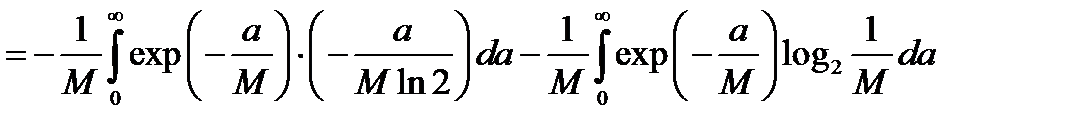 .
.
После преобразований и взятия интегралов (там, где нужно при помощи таблиц интегралов) получим: 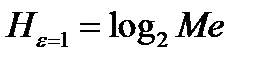 .
.
Дата добавления: 2021-04-21; просмотров: 642;











