Примеры с решениями

Пример 1.Вычислить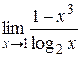

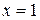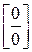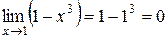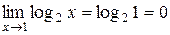Решение. Подстановка предельного значения аргумента приводит к неопределенности , т.е. выполняется первое условие теоремы: и . Второе условие теоремы тоже выполняется, поскольку функци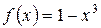и и 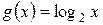дифференцируемы в некоторой окрестности точки 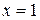, причем для любого 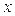из этой окрестности (в качестве окрестности можно рассмотреть, например, интервал 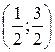). Выполняется и третье условие: существует предел отношения производных этих функций 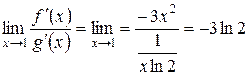. Итак, решение этой задачи можно коротко записать следующим образом:

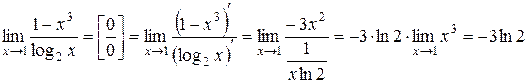
Ответ: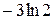

Пример 2. Вычислить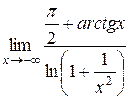

Решение.

Ответ: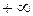

Пример 3. Вычислить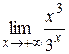

Решение.

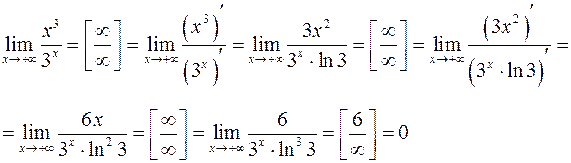
Ответ: 0

Пример 4. Вычислить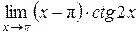

Решение.

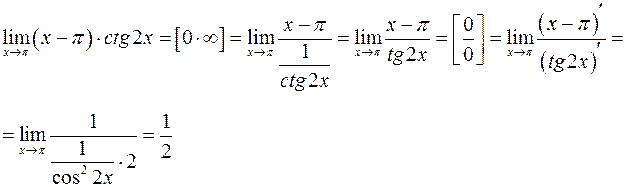
Ответ: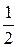

Пример 5. Вычислить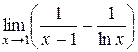

Решение.

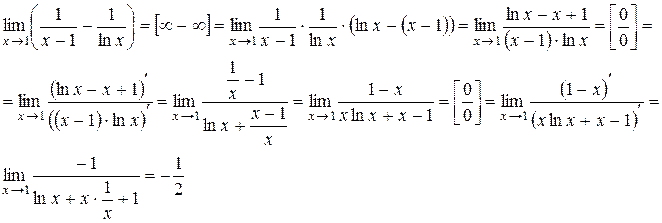
Ответ: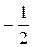

Пример 6. Вычислить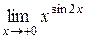

Решение.

Рассмотрим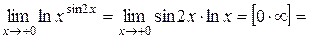

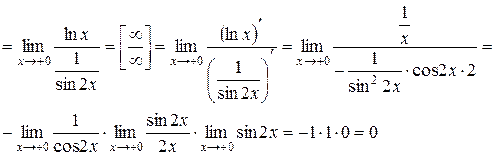
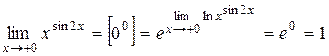
Ответ: .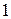

Пример 7. Вычислить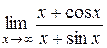

Решение. Перед нами неопределенность 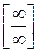, в числителе дроби мы видим функции, дифференцируемые на всем множестве действительных чисел, но отношение производных 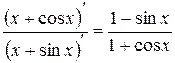не имеет предела при 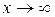. Однако, это не значит, что исходный предел не существует, его можно вычислить без использования правила Лопиталя, применяя лишь тождественные преобразования и свойства пределов:

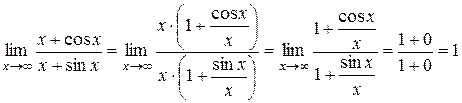
Ответ: 1.

Пример 8. Вычислить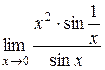

Решение. Правило Лопиталя не применимо, так как при 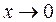предел отношения производных 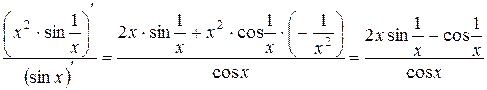не существует. Но задача имеет решение:

Ответ: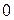

Пример 9. Вычислить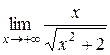

Решение.

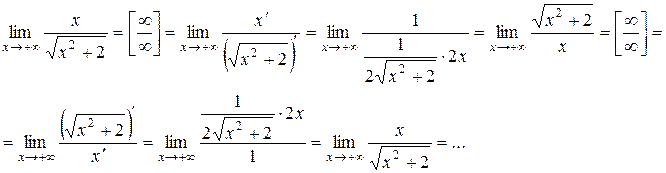
Правило Лопиталя не приводит нас к решению этой задачи, но искомый предел существует и его легко вычислить, разделив числитель и знаменатель дроби на x:

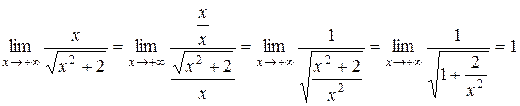
Ответ: