Раскрытие неопределённостей. Правило Лопиталя
При решении задач, связанных с вычислением пределов функций, часто непосредственная подстановка предельного значения аргумента приводит к неопределённым выражениям вида: 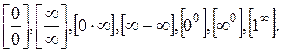 Нахождение предела в таких случаях называют раскрытием соответствующей неопределенности. Довольно часто справиться с этой проблемой помогает так называемое правило Лопиталя, которое можно сформулировать в виде теоремы.
Нахождение предела в таких случаях называют раскрытием соответствующей неопределенности. Довольно часто справиться с этой проблемой помогает так называемое правило Лопиталя, которое можно сформулировать в виде теоремы.
Теорема. Если функции 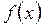 и
и 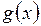 удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
1) 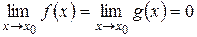 или
или 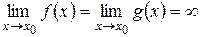 ;
;
2) 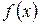 и
и 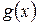 дифференцируемы в некоторой окрестности точки
дифференцируемы в некоторой окрестности точки 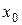 , и
, и  для любого
для любого 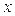 их этой окрестности (за исключением, может быть, самой точки
их этой окрестности (за исключением, может быть, самой точки 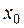 );
);
3) существует (конечный или бесконечный) 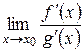 , то тогда
, то тогда
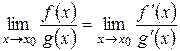 .
.
Замечание 1. Если 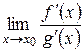 не существует, то нельзя ничего сказать об исходном пределе, т.е.
не существует, то нельзя ничего сказать об исходном пределе, т.е. 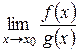 может существовать, а может и не существовать. В такой ситуации решать задачу вычисления предела надо без использования правила Лопиталя.
может существовать, а может и не существовать. В такой ситуации решать задачу вычисления предела надо без использования правила Лопиталя.
Замечание 2. Правилом Лопиталя можно пользоваться (в случае выполнения условий теоремы) при раскрытии неопределенностей вида 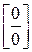 или
или 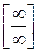 не только при
не только при  , но и при
, но и при 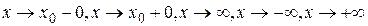 .
.
Замечание 3. Правило Лопиталя в некоторых задачах можно применять повторно.
Если необходимо раскрыть неопределенности иного вида, нежели 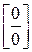 и
и 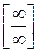 , то следует преобразовывать функцию, стоящую под знаком предела, приведя её к виду, позволяющему применить правило Лопиталя.
, то следует преобразовывать функцию, стоящую под знаком предела, приведя её к виду, позволяющему применить правило Лопиталя.
Если при 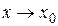
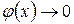 , а
, а 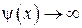 , то вычисление предела
, то вычисление предела 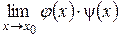 (неопределенность вида
(неопределенность вида 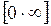 ) может быть сведено к одному из случаев
) может быть сведено к одному из случаев 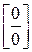 или
или 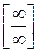 при помощи тождественных преобразований произведения в частное:
при помощи тождественных преобразований произведения в частное:
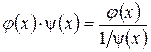 или
или 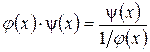
Если при 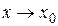
 , а
, а 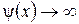 , то вычисление предела
, то вычисление предела 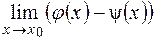 (неопределенность вида
(неопределенность вида 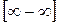 ) может быть сведено к раскрытию неопределенности
) может быть сведено к раскрытию неопределенности 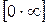 путем тождественного преобразования разности в произведение:
путем тождественного преобразования разности в произведение:
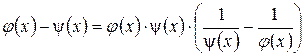 .
.
Иногда удобно пользоваться и другими преобразованиями:
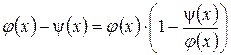 или
или 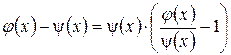
При вычислении пределов вида 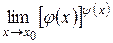 можно столкнуться с неопределенностью
можно столкнуться с неопределенностью 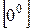 или
или 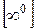 , или
, или 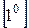 . Раскрытие этих неопределенностей производят с помощью следующего преобразования:
. Раскрытие этих неопределенностей производят с помощью следующего преобразования:
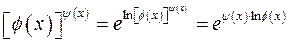
Тогда (в силу непрерывности показательной функции) получают: 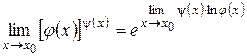 , что сводит задачу к неопределенности
, что сводит задачу к неопределенности 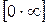 или
или  .
.
Дата добавления: 2017-01-08; просмотров: 1554;











