Примеры с решениями
Пример 1. Найти интервалы возрастания и убывания функции 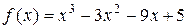 .
.
Решение. Область определения функции 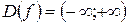 . Находим производную
. Находим производную 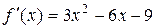 . Для нахождения интервалов возрастания функции решаем неравенство
. Для нахождения интервалов возрастания функции решаем неравенство 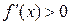 ,
, 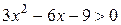 ,
, 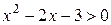 , получаем
, получаем 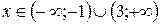 , на этих интервалах функция возрастает. Для нахождения интервалов убывания решаем неравенство
, на этих интервалах функция возрастает. Для нахождения интервалов убывания решаем неравенство 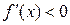 ,
, 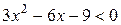 ,
, 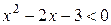 , получаем
, получаем 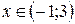 , на этом интервале функция убывает.
, на этом интервале функция убывает.
Можно поступить и так: находим точки, в которых 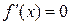 ,
, 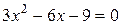 ,
, 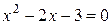 ,
, 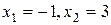 . Эти точки отметим на числовой прямой и определим знаки производной на образовавшихся интервалах:
. Эти точки отметим на числовой прямой и определим знаки производной на образовавшихся интервалах:
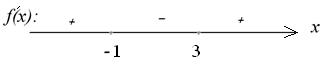
Интервалы, на которых производная функции имеет знак «+», являются интервалами возрастания функции, а те, на которых «−» − интервалами убывания.
Ответ: функция возрастает на интервале 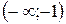 и
и 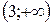 ; функция убывает на интервале
; функция убывает на интервале 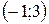
Пример 2. Найти интервалы монотонности функции 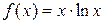
Решение. Область определения функции 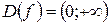 . Находим производную
. Находим производную 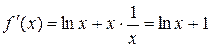 , решаем уравнение
, решаем уравнение 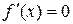 ,
,
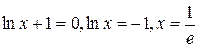 .
.
Изображаем область определения функции и наносим на нее точку 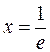 , после чего определяем знак производной на каждом из образовавшихся интервалов:
, после чего определяем знак производной на каждом из образовавшихся интервалов:
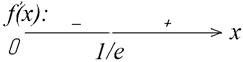
Теперь видим, что на интервале 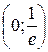 функция убывает, а на интервале
функция убывает, а на интервале 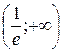 возрастает.
возрастает.
Ответ: функция возрастает на интервале 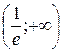 , убывает на интервале
, убывает на интервале 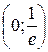
Пример 3. Найти экстремумы функции 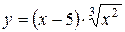
Решение. Область определения функции 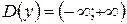 . Находим производную
. Находим производную 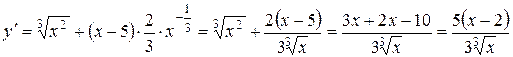 . Находим критические точки:
. Находим критические точки: 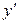 не существует при
не существует при 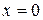 ,
, 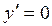 при
при 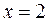 .
.
Изображаем область определения функции (это вся числовая прямая) и наносим на нее критические точки, после чего определяем знак производной на каждом из образовавшихся интервалов:
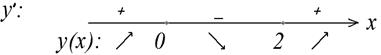
По знаку производной на каждом интервале определяем характер монотонности функции и видим точки экстремума. Остается вычислить сами экстремумы функции: 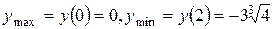 .
.
Ответ: 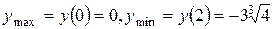
Пример 4. Найти экстремумы функции 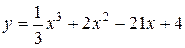 .
.
Решение.
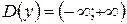
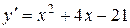
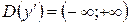
Критические точки: 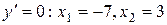
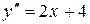
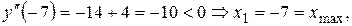
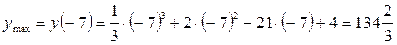
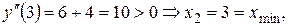
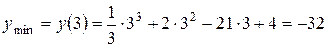
Ответ: 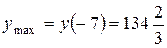 ,
, 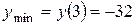 .
.
Дата добавления: 2017-01-08; просмотров: 2923;











