Примеры с решениями
Пример 1. Найти 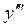 от функции
от функции 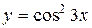
Решение.
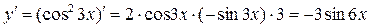
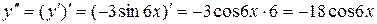
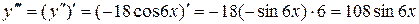
Ответ: 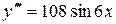
Пример 2. Найти производную n-го порядка от функции 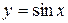
Решение. Определяем последовательно 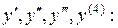
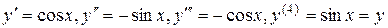
Мы установили закон, по которому строятся последовательные производные от 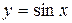 . Теперь можно дать и общую формулу для n-й производной от этой функции. Действительно,
. Теперь можно дать и общую формулу для n-й производной от этой функции. Действительно,
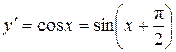
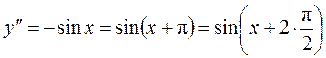
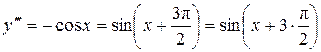
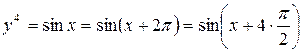
______________________________
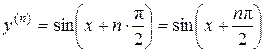
Ответ: 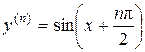
Пример 3. Найти производную третьего порядка от функции 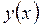 , заданной параметрически уравнениями
, заданной параметрически уравнениями 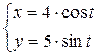
Решение.
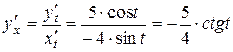
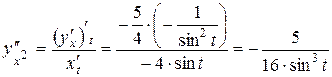
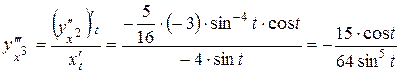
Ответ: 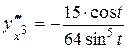
Пример 4. Найти производную n-го порядка от функции 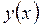 , если она задана параметрически уравнениями
, если она задана параметрически уравнениями 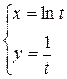
Решение.
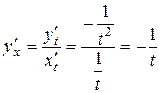
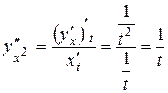
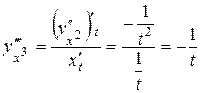 и т.д.
и т.д.
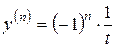
Ответ: 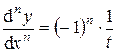
Пример 5. Найти производную второго порядка от функции 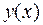 , заданной неявно уравнением
, заданной неявно уравнением 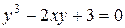
Решение. Найдем 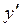 , продифференцировав по
, продифференцировав по 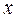 обе части уравнения, задающего неявно функцию
обе части уравнения, задающего неявно функцию 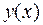 , рассматривая при этом
, рассматривая при этом 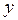 как функцию от
как функцию от 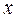 .
.
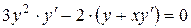
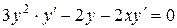
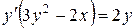
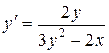
Теперь продифференцируем по 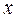 обе части полученного равенства (рассматривая
обе части полученного равенства (рассматривая 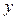 как функцию от
как функцию от 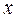 ).
).
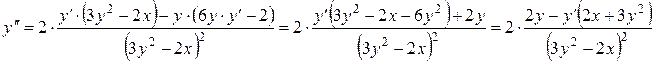
И теперь в полученное выражение подставим 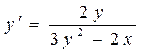 :
:
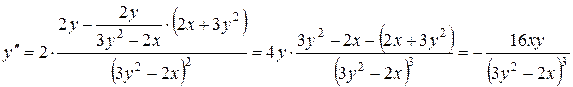
Ответ: 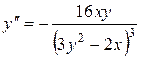
Пример 6. Найти дифференциал 22-го порядка функции 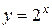
Решение.
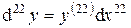
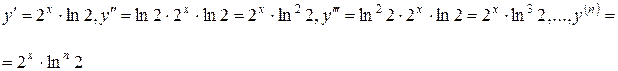
Следовательно, 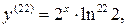 тогда
тогда 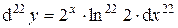
Ответ: 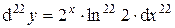
Дата добавления: 2017-01-08; просмотров: 1232;











