Примеры с решениями

Пример 1. Найти наименьшее и наибольшее значения функции 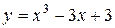на отрезке .

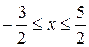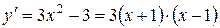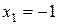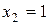Решение. Находим . Отсюда видим, что критические точки: и . Находим значения функции в этих точках и на концах данного отрезка:

.

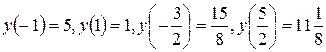Из полученного следует, что 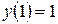− наименьшее, а 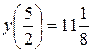− наибольшее значение функции на заданном отрезке.

Ответ: наименьшее значение 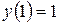, наибольшее значение .

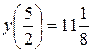Пример 2. Имеется смесь, состоящая из двух газов: оксида азота и кислорода. При какой концентрации кислорода содержащийся в смеси оксид азота окисляется с максимальной скоростью?

Решение. При наличии условий критической необратимости можно считать, что скорость реакции 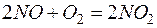выражается формулой 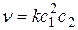, где 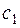– концентрация 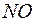в момент времени 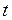; 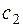– концентрация 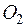; 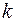– константа скорости, зависящая только от температуры. Выражая концентраци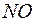и и 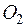в объёмных процентах, будем иметь 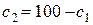, 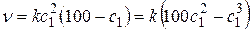. Находим первую производную 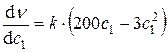и, приравнивая её к нулю: 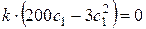. Найдём .

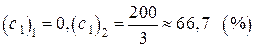Найдем вторую производную: 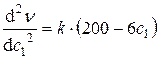, так как 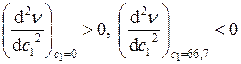, то заключаем, что при 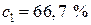скорость окисление имеет максимум. Далее, так как при 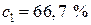, , 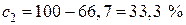то заключаем, что скорость окисления азота имеет максимум, если кислорода в газовой смеси содержится 33,3 %.

Ответ: При концентрации кислорода 33,3 %.

Пример 3. Требуется изготовить фильтр путём вырезания из круга радиуса 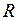сектора и свёртывания последнего в конус. При каком центральном угле сектора объём фильтра будет наибольшим?

Решение. Обозначим угол сектора через 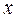, а радиус окружности основания конуса через 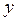. Тогда 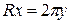, откуда 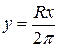. Если высота

фильтра 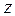, то объём его ,

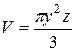где 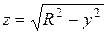или .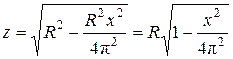

Поэтому .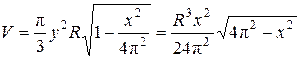

Итак, 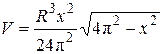− функция от 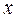, наибольшее значение которой на отрезке 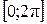нужно найти. Находим первую производную и приравняем её к нулю:

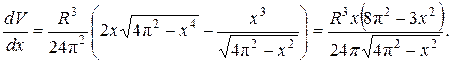
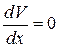, если 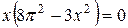, откуда, рассматривая только то решение, которое имеет смысл, находим .

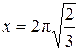По смыслу задачи ясно, что при 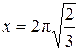фильтр будет иметь наибольший объём, равный:

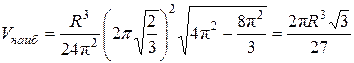
Ответ: при 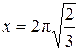фильтр будет иметь наибольший объём.