Производные и дифференциалы высших порядков

Производная 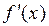от функции 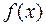называется производной первого порядка или первой производной и представляет собой некоторую функцию, которая также может иметь производную. Тогда производная от производной первого порядка называется производной второго порядка или второй производной. Ее обозначают одним из следующих символов:

.

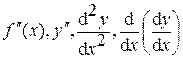Производная от производной второго порядка, если она существует, называется производной третьего порядка или третьей производной. Аналогично определяются производные четвертого, пятого и т.д. порядков. Вообще, производной n-го порядка от функции 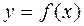называется производная от производной (n–1)-го порядка:

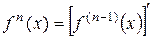
Производные высших порядков вычисляются последовательным дифференцированием функции.

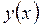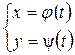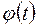Если функция задана параметрически системой уравнений: , где и 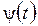− дифференцируемые функции и 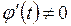, то для нахождения производных функции 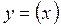можно использовать следующие формулы:

и т.д.

Производную второго порядка можно также вычислить по формуле:

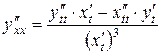
Для нахождения второй производной от функции, заданной неявно, равенство 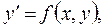задающее ее первую производную, дифференцируют по 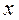(рассматривая 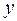как функцию от 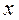), а затем в правой части полученного равенства на место 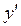подставляют задающее ее выражение 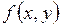. Аналогично поступают при нахождении производных более высоких порядков.

Дифференциалом второго порядка функции 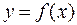называется дифференциал от дифференциала первого порядка этой функции:

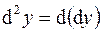
Аналогично определяется дифференциал третьего порядка:

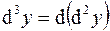
Вообще, .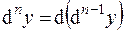

Есл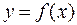и и 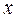– независимая переменная, то дифференциалы высших порядков вычисляются по формулам:

­­­_________

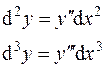
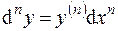
Свойством инвариантости дифференциалы высших порядков (начиная со второго) не обладают.