Примеры для самостоятельного решения
Определить вид кривой, заданной параметрически системой уравнений, и нарисовать её.
7.1. 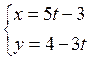
7.2. 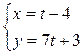
7.3. 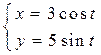
7.4. 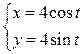
7.5. 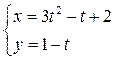
7.6. 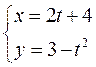
Найти производную функции y = y(x), заданной параметрически системой уравнений
7.7. 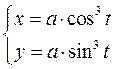
7.8. 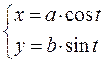
7.9. 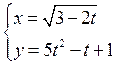
7.10. 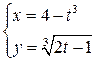
7.11. 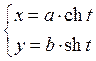
7.12. 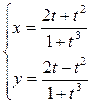
7.13. Составить уравнения касательной и нормали к циклоиде 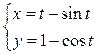 , проведенных в точке, для которой t =
, проведенных в точке, для которой t = 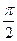 .
.
7.14. Составить уравнения касательной и нормали к астроиде 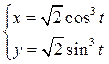 ,
,
проведенных в точке, для которой t = 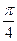 .
.
7.15. Составить уравнения касательной и нормали к эллипсу 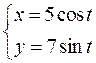 ,
,
проведенных в точке, для которой t = 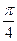 . Сделать чертёж.
. Сделать чертёж.
7.16. Составить уравнения касательной и нормали к эллипсу 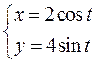 ,
,
проведенных в точке, для которой t = 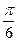 . Сделать чертёж.
. Сделать чертёж.
7.17. Составить уравнения касательной и нормали к кривой, заданной параметрически системой уравнений 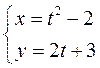 ,
,
проведенных в точке М0 (–1;1)
7.18. Составить уравнения касательной и нормали к кривой, заданной параметрически системой уравнений 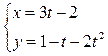 ,
,
проведенных в точке М0 (1;–2)
Ответы
7.1. 3x + 5y – 11= 0 – уравнение прямой; 7.2. y = 7x + 31 – уравнение прямой;
7.3. 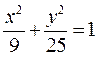 – уравнение эллипса; 7.4.
– уравнение эллипса; 7.4. 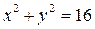 – уравнение окружности; 7.5.
– уравнение окружности; 7.5. 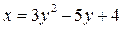 – уравнение параболы; 7.6.
– уравнение параболы; 7.6. 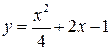 –уравнение параболы; 7.7.
–уравнение параболы; 7.7. 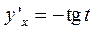 ; 7.8.
; 7.8. 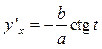 ;
;
7.9. 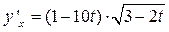 ; 7.10.
; 7.10. 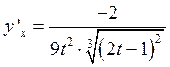 ;7.11.
;7.11. 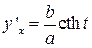 ;
;
7.12. 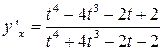 ;7.13.
;7.13. 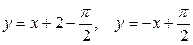 ;7.14. y =
;7.14. y = 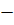 x+1, y = x;
x+1, y = x;
7.15. 7x+5y 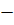 35
35 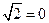 , 5x
, 5x 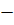 7y+12
7y+12 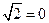 ; 7.16. 2
; 7.16. 2 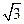 x+y–8=0,
x+y–8=0, 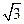 x
x 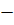 6y+9=0;
6y+9=0;
7.17. y = 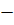 x, y = x + 2; 7.18. 5x+3y+1=0, 3x
x, y = x + 2; 7.18. 5x+3y+1=0, 3x 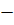 5y
5y 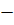 13=0.
13=0.
Дата добавления: 2017-01-08; просмотров: 1432;











