Дифференциал функции

Функция y = f(x) называется дифференцируемой в точке х₀ , если её приращение в этой точке, соответствующее приращению аргумента ∆х, может быть представлено в виде

∆y = A·∆x+α(∆x)· ∆x, (1)

где А – число, не зависящее от ∆x (А зависит от х₀ ), α(∆x) – бесконечно малая функция при ∆x→0.

Дифференциалом этой функции в точке х₀ называется главная часть её приращения функции А·∆x (линейная относительно приращения аргумента). Для того чтобы функция y = f(x) была дифференцируемой в точке х₀, необходимо и достаточно, чтобы существовала конечная производная 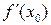; при этом справедливо равенство 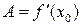. Этот факт позволяет называть дифференцируемой всякую функцию, имеющую конечную производную. Выражение для дифференциала функции y = f(x) в точке х₀ имеет вид

dy(х₀) = f '(х₀)· ∆x. (2)

Для независимой переменной х её приращения совпадает с её дифференциалом: ∆x = dx. Таким образом, для вычисления дифференциала функции используют формулу

dy= f '(х)· dx. (3)

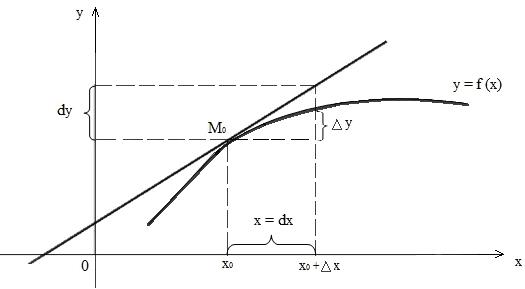
Геометрически дифференциал функции y = f(x) в точке х₀ равен приращению ординаты касательной к графику этой функции в точке М₀(х₀; f(х₀)) при приращении аргумента ∆x.