Примеры с решениями
Пример 1. Функция 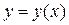 задана неявно уравнением
задана неявно уравнением 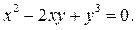
Найти 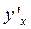 .
.
Решение. Поскольку у является функцией от х, будем рассматривать y³ как сложную функцию от х, следовательно, 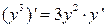 . Продифференцировав по х обе части заданного уравнения, получим:
. Продифференцировав по х обе части заданного уравнения, получим:
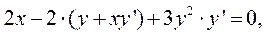
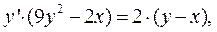
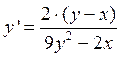
Ответ: 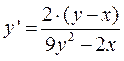 .
.
Пример 2. Найти производную функции 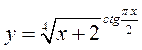 .
.
Решение. В данном примере при нахождении производной удобно от явного задания функции перейти к неявному. Прологарифмируем обе части равенства, задающего функцию (при этом обычно используют натуральный логарифм):
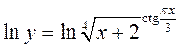
Используя свойства логарифмов, позволяющее показатель степени вынести множителем за знак логарифма, получим неявно заданную функцию у в форме,
удобной для дифференцирования:
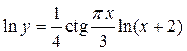
Продифференцируем по х обе части полученного уравнения.
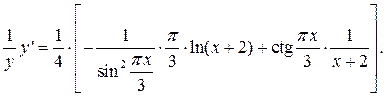
Выразим y′, домножив обе части этого уравнения на 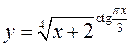
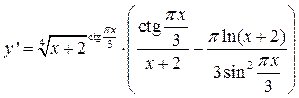
Ответ: 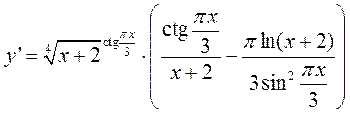
Производную от логарифма функции называют логарифмической производной.
Пример 3. Найти производную функции
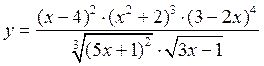 .
.
Решение. Отметим, что данная функция на своей области определения 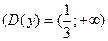 принимает положительные значения. Воспользуемся логарифмической производной и свойствами логарифмов:
принимает положительные значения. Воспользуемся логарифмической производной и свойствами логарифмов:
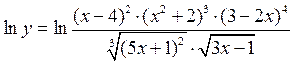
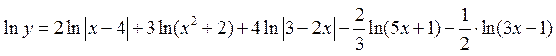
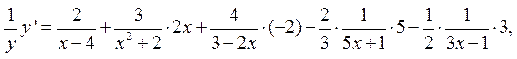
из этого равенства найдём 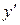 ,умножив обе его части на
,умножив обе его части на
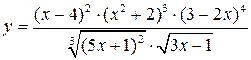 .
.
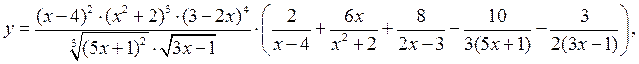
Ответ: 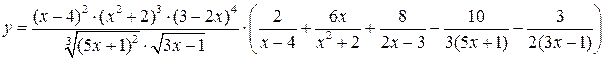 .
.
Пусть у есть функция от аргумента x:
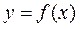 (1)
(1)
Задавая значения 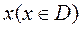 , по формуле (1)будем получать соответствующие значения
, по формуле (1)будем получать соответствующие значения 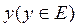 . Можно, однако, считать у независимой переменной, а x – зависимой, задавать значения у и вычислять соответствующие им значения x. И если каждому значению у будет соответствовать единственное значение x, то равенство (1)можно рассматривать как неявное задание функции х от аргумента у. Такая функция называется обратной по отношению к данной функции у. Если уравнение (1)разрешить относительно х, получим явное выражение обратной функции, её обозначают
. Можно, однако, считать у независимой переменной, а x – зависимой, задавать значения у и вычислять соответствующие им значения x. И если каждому значению у будет соответствовать единственное значение x, то равенство (1)можно рассматривать как неявное задание функции х от аргумента у. Такая функция называется обратной по отношению к данной функции у. Если уравнение (1)разрешить относительно х, получим явное выражение обратной функции, её обозначают 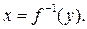
И для всех допустимых значений у будет выполняться равенство
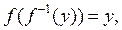 (2)
(2)
которое можно рассматривать как уравнение, задающее функцию 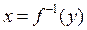 неявно.
неявно.
Для вычисления производной функции 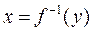 продифференцируем уравнение (2) по у:
продифференцируем уравнение (2) по у:
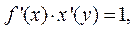
Откуда 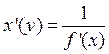 или
или 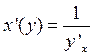 , если
, если 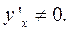
Таким образом, для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной
данной функции.
Пример 4. Вывести формулу производной функции 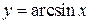
Решение. Рассмотрим функцию 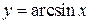 ,где
,где 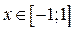 ,
, 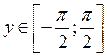 .
.
Обратная к ней функция имеет вид 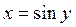 , причём
, причём 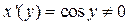 при
при 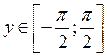 . Воспользовавшись правилом дифференцирования обратной функции, получим
. Воспользовавшись правилом дифференцирования обратной функции, получим
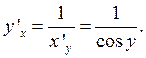
Поскольку cos y > 0 для всех 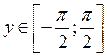 , то, учитывая, что
, то, учитывая, что 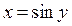 , получаем
, получаем 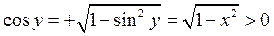 , при
, при 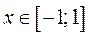 . Следовательно:
. Следовательно:
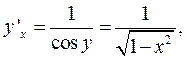
т.е. 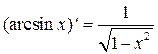 , где
, где 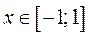
Ответ: 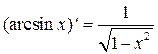 , где
, где 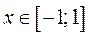 .
.
Пример 5.Вывести формулу производной функции, обратной к функции 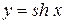 .
.
Решение. Дана функция 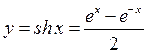 , её производная
, её производная 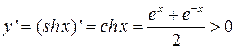 , для всех
, для всех 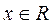 ,следовательно, функция
,следовательно, функция 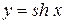 на всей действительной оси монотонно возрастает и имеет обратную функцию, обозначаемую
на всей действительной оси монотонно возрастает и имеет обратную функцию, обозначаемую 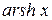 .
.
Уравнение 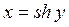 задаёт эту обратную функцию неявным образом. Продифференцируем обе части по х:
задаёт эту обратную функцию неявным образом. Продифференцируем обе части по х: 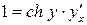 , откуда
, откуда 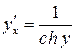 .
.
Из соотношения 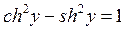 выразим
выразим 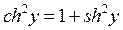 , а поскольку
, а поскольку 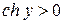 для всех
для всех 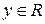 , тополучим
, тополучим 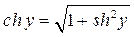 , где
, где 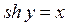 .
.
Таким образом, 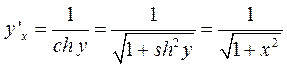 .
.
Итак, формула производной функции, обратной к гиперболическому синусу, имеет вид:
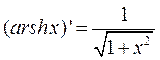
Ответ: 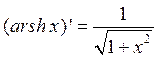 .
.
Дата добавления: 2017-01-08; просмотров: 1538;











