Примеры для самостоятельного решения
3.1. Вычислить приращение функции 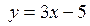 в точке
в точке 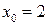 , соответствующее приращению аргумента
, соответствующее приращению аргумента 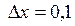 .
.
3.2. Вычислить приращение функции 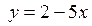 в точке
в точке  , соответствующее приращению аргумента
, соответствующее приращению аргумента 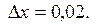
3.3. Найти приращение функции 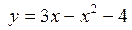 в точке
в точке  для любого приращения аргумента
для любого приращения аргумента 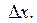
3.4. Найти приращение функции 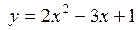 в точке x = 2 для любого приращения аргумента
в точке x = 2 для любого приращения аргумента 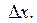
3.5. Пользуясь определением производной, вычислить 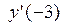 для функции
для функции  .
.
3.6. Пользуясь определением производной, вычислить 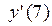 для функции
для функции  .
.
3.7. Пользуясь определением производной, вывести формулу производной функции 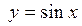 в любой точке,
в любой точке, 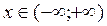 и найти значения этой производной в точках:
и найти значения этой производной в точках: 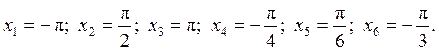
3.8. Пользуясь определением производной, вывести формулу производной функции 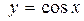 в любой точке,
в любой точке, 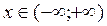 и найти значения этой
и найти значения этой
производной в точках: 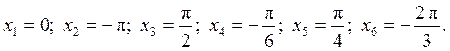
3.9. Найти угловой коэффициент касательной к графику функции 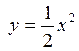 в точке M(2;2), составить уравнения касательной и нормали к этой кривой в точке M, сделать чертеж.
в точке M(2;2), составить уравнения касательной и нормали к этой кривой в точке M, сделать чертеж.
3.10. Составить уравнения касательной и нормали к графику функции 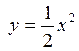 в точке с абсциссой x0 = 2 . Сделать чертеж.
в точке с абсциссой x0 = 2 . Сделать чертеж.
3.11. На графике функции 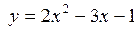 найти точку, касательная к которой параллельна биссектрисе первого координатного угла. Составить уравнение этой касательной. Сделать чертеж.
найти точку, касательная к которой параллельна биссектрисе первого координатного угла. Составить уравнение этой касательной. Сделать чертеж.
3.12. На графике функции 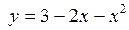 найти точку, касательная к которой перпендикулярна прямой
найти точку, касательная к которой перпендикулярна прямой 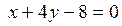 . Составить уравнение этой касательной. Сделать чертеж.
. Составить уравнение этой касательной. Сделать чертеж.
3.13. Составить уравнения касательных к графику функции 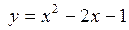 , приходящих через точку A(2;2). Сделать чертеж.
, приходящих через точку A(2;2). Сделать чертеж.
3.14. Закон движения точки: 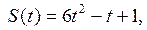 где S – расстояние в метрах, t – время в секундах. Найти скорость этой точки в момент времени t = 4.
где S – расстояние в метрах, t – время в секундах. Найти скорость этой точки в момент времени t = 4.
Ответы
3.1.  ; 3.2.
; 3.2.  ;3.3.
;3.3. 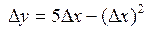 ; 3.4.
; 3.4. 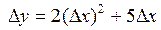 ;
;
3.5. – 4; 3.6. – 4; 3.7. 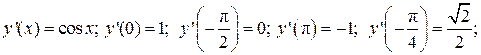
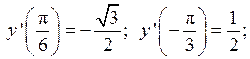 3.8.
3.8. 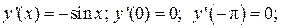
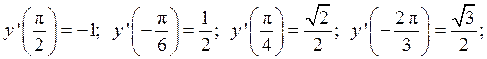
3.9. 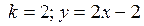 – уравнение касательной;
– уравнение касательной; 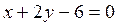 – уравнение нормали; 3.10.
– уравнение нормали; 3.10. 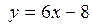 – уравнение касательной;
– уравнение касательной;  – уравнение нормали; 3.11.
– уравнение нормали; 3.11. 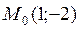 – точка касания;
– точка касания;  – уравнение касательной; 3.12.
– уравнение касательной; 3.12. 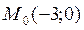 – точка касания;
– точка касания;  – уравнение касательной; 3.13.
– уравнение касательной; 3.13. 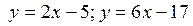 ;3.14.
;3.14. 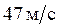 .
.
Дата добавления: 2017-01-08; просмотров: 1282;











