Некоторые методы вычисления пределов

1. Случай отсутствия неопределённости

Если при подстановке предельного значения аргумента в функцию получается определённое число, то оно и является значением предела.

Пример 2. Вычислить предел:

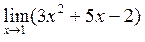
Решение.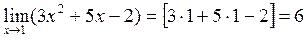

Ответ: 6.

Пример 3. Вычислить предел:

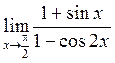
Решение.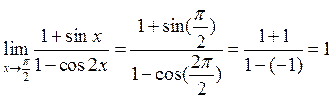

Ответ: 1.

Пример 4. Вычислить предел:

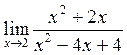
Решение.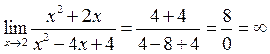

Ответ: .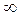

Если в результате формальной подстановки в функцию предельного значения аргумента предел переходит в выражение типа:

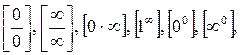
то говорят, что под знаком предела неопределённость.

В этом случае нужно раскрыть неопределённость: тождественными преобразованиями «убирают» неопределённость, если это возможно, и вычисляют предел.

2. Случай неопределённости вида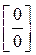

Если в пределе 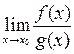приходим к неопределённости вида 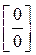, то

необходимо в числителе и знаменателе дроби выделить сомножитель 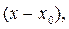сократить на него и вычислить предел.

Пример 5.Вычислить предел:

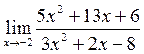
Решение. Имеем неопределённость вида 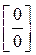. Для её раскрытия разложим числитель и знаменатель дроби на множители и сократим на общий множитель 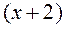(вспомним, что 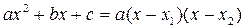, где 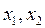– корни уравнения ).

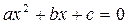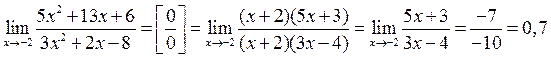
Ответ: 0,7.

Раскрытие неопределённости вида 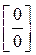с иррациональностями

Рассмотрим на примере.

Пример 6. Вычислить предел:

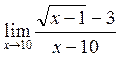
Решение. Имеем неопределённость вида 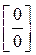. Домножим числитель и знаменатель дроби, предел которой мы ищем, на выражение 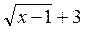, сопряжённое числителю.

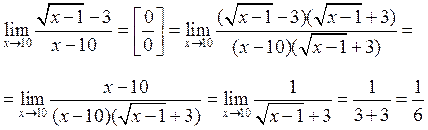
Ответ: .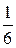

Для пределов подобного вида способ домножения на сопряжённое выражение является типичным.

3. Случай неопределённости вида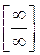

Для раскрытия исходной неопределённости нужно разделить числитель и знаменатель дроби на переменную xв наибольшей степени, которая входит в данную дробь, учитывая, что величина обратная бесконечно большой есть бесконечно малая величина.

Пример 7. Вычислить предел:

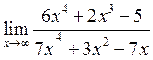
Решение. Имеем неопределённость вида 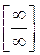. Разделим числитель и знаменатель дроби на .

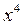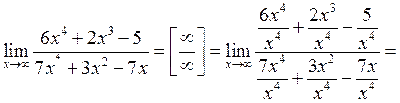
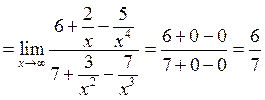
Ответ: .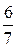

В общем случае можно использовать правило:

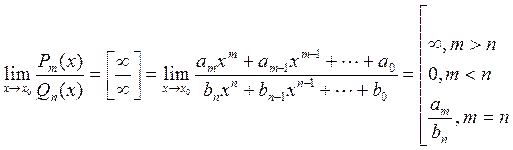
4. Случай неопределённостей вида: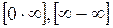

Эти неопределённости сводятся к неопределённостям вида 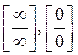одним из следующих способов:

а) приведение дробей к общему знаменателю,

б) преобразование функции к виду дроби,

в) избавление от иррациональности (домножение на сопряжённое выражение числителя и знаменателя дроби).

Пример 8. Вычислить предел:

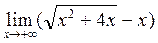
Решение.

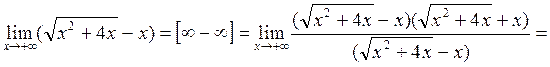
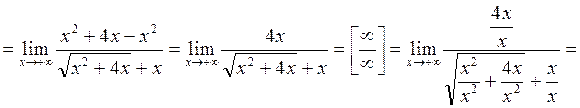
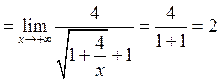
Ответ: 2.