Предел функции на бесконечности
Предел функции. Вычисление предела функции с помощью алгебраических преобразований
Пусть функция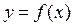 
определена в некоторой окрестности точке 
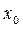, кроме, быть может, самой точки .
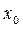Определение 1. Число A называется пределом (по Коши) функции 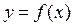в точке 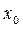(или при 
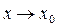), если для любого числа 
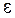> 0 найдётся отвечающее ему положительное число d такое, что для всех значений, удовлетворяющих условию 
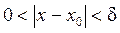, справедливо неравенство: 
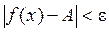. При этом записывают:
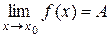(или 
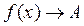при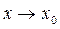 
).
Примеры с решениями
Пример 1.Используя определения, доказать, что функция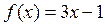 
в точке 
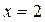имеет предел, равный 5, т.е. 
.
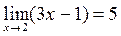Решение. Возьмём любое 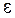>0 . Задача состоит в том, чтобы для этого 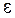найти такое d > 0, при котором из неравенства 
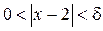следовало бы неравенство 
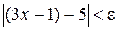. Преобразуя последнее неравенство, получаем 
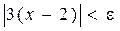, или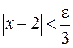 
. Отсюда видно, если взять 
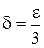, то для всех 
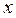, удовлетворяющих неравенству 
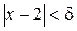, выполняется требуемое неравенство 
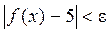. Это и означает, что 
.
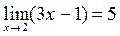Предел функции на бесконечности
Определение 2. Число A называется пределом функции 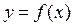при 
( 
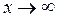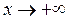или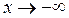 
), если для любого положительного числа ε существует отвечающее ему положительное число M такое, что для всех 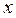, удовлетворяющих неравенству 
( 
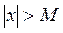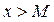или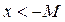 
), выполняется неравенство: 
.
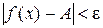При этом записывают:
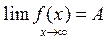
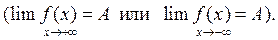
Дата добавления: 2017-01-08; просмотров: 1065;
Поиск по сайту
Узнать еще
- CIH — газораспределительный механизм с распределительным валом в головке блока цилиндров
- Cвойства определителей
- F-распределение Фишера
- I. Общие принципы структурно-функциональной организации клетки и её компоненты. Плазмолемма, её структура и функции.
- I.1.6 ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. ЗАКОН РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ
- I.1.7 СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
- II. Митохондрии (строение и функции)
- II. Признаки, ресурсы и функции власти.
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
