Опыты Фарадея. Закон электромагнитной индукции. Вих-ревое электрическое поле.
Явление электромагнитной индукции было открыто Фарадеем в
1831 г. и заключается в следующем: во всяком замкнутом проводя-щем контуре при изменении потока магнитной индукции через пло-щадь, ограниченную этим контуром, возникает электрический ток. Этот ток называется индукционным. Рассмотрим некоторые опытына основании которых и было открыто это явление.
| S | |||
| N | К2 | Г | |
| Г | |||
| Б | К1 |
К
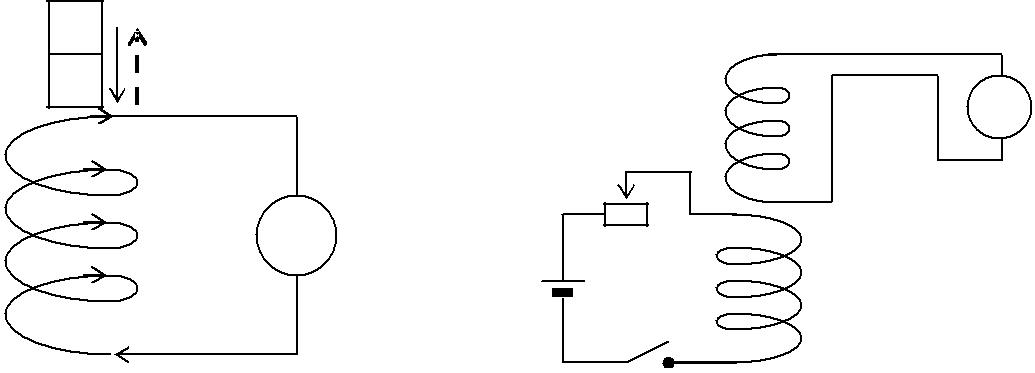
Рис. 3.1.1
В первом опыте на рис. 3.1.1, если в катушку, замкнутую на галь-ванометр, вдвигать или выдвигать из нее постоянный магнит, наблю-дается отклонение влево или вправо стрелки гальванометра, т. е. воз-никает индукционный ток. Причем следует отметить, что отклонения стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки . При изменении полюсов магнита на-правление отклонения стрелки изменится. Индукционный ток возни-кает в катушке также и в том случае, если постоянный магнит непод-вижен, а катушка движется. Во втором опыте (рис. 3.1.1) используют
две катушки (К1 и К2), которые могут быть вставлены одна в другую. Катушка К1 подключена через реостат и ключ к источнику электро-энергии, а катушка К2 подсоединена к гальванометру. Стрелка гальва-нометра будет отклоняться при замыкании или размыкании цепи с ка-тушкой К1, в моменты увеличения или уменьшения электрического тока в цепи, а также при перемещении катушек относительно друг друга. Направление отклонения стрелки гальванометра влево или вправо определяется увеличением и уменьшением электрического то-ка, его включением и выключением, а также сближением или удале-нием катушек друг от друга.
На основании опытов М. Фарадей пришел к выводу, что индук-ционный ток в замкнутом контуре возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции, а ве-личина индукционного тока определяется скоростью изменения по-тока магнитной индукции и не зависит от способа его изменения. При этом э. д. с. индукции равна:
| εi = | dФm | − закон Фарадея. | (3.1.1) | |
| dt | ||||
Это уравнение справедливо независимо от того, чем вызвано из-менение потока индукции через контур: изменением его формы, его поворотом, перемещением в неоднородном поле или изменением со временем магнитной индукции самого поля.
Русский физик Э. Х. Ленц , который исследовал взаимосвязь на-правления индукционного тока и причины, вызывающей ток, в 1833 г. установил закономерность, называемую правилом Ленца: при всяком изменении магнитного потока сквозь поверхность, ограниченную замкнутым контуром, в последнем возникает индукционный ток, ко-торый имеет такое направление, что его собственное магнитное по-ле препятствует изменению внешнего магнитного потока, вызы-вающего этот индукционный ток.
В 1845−1847 гг. Ф. Нейман создал теорию электромагнитной ин-дукции и получил математическое выражение для закона, который объединил закон Фарадея и правило Ленца и который был назван за-коном Фарадея – Ленца:
| εi = − | dФm | . | (3.1.2) | |
| dt |
Э. д. с. индукции в проводящем контуре численно равна и проти-воположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
Рассмотрим контур, состоящий из N витков, в котором индуциру-ется э. д. с. Поскольку витки соединяются последовательно, то э. д. с., возбуждаемые в каждом витке, будут складываться. Поэтому
| N | d Φ | m | d | N | |||||||
| εi = − ∑ | = − | ∑Φm . | (3.1.3) | ||||||||
| dt | |||||||||||
| k =1 | dt k =1 | ||||||||||
| N | |||||||||||
| Величину Ψ = ∑Φ mi = N·Φm | называют потокосцеплением. | ||||||||||
| k =1 | |||||||||||
| εi = − | d Ψ | = −N | dΦm | . | (3.1.4) | ||||||
| dt | dt | ||||||||||
Уравнение (3.1.4) выражает закон электромагнитной индукции для контура из N витков.
Э. д. с. электромагнитной индукции в контуре условно считают положительной, если магнитный момент pm соответствующего ей ин-дукционного тока образует острый угол с линиями магнитной индук-ции того поля, которое возбуждает этот ток. На рис. 3.1.2, а, εi < 0, а
на рис. 3.1.2, б, εi > 0.
| dФm | > 0 | dФ | m | < 0 | |
| dt | |||||
| Pm | dt | ||||
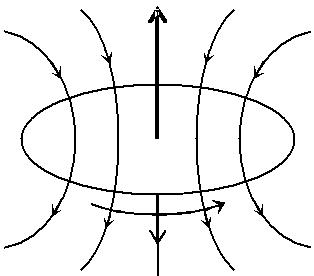
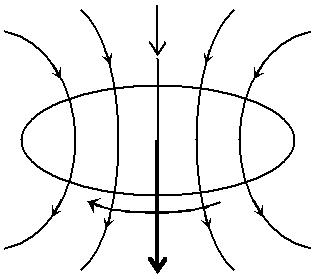
Pm
а б
Рис. 3.1.2
Хотя величина э. д. с. индукции и не зависит от способа изменения магнитного потока, однако механизм ее возникновения при этом оказы-вается разным. Обратимся сначала к случаю, когда поток изменяется вследствие движения проводящего контура (или изменения его геомет-рии) в постоянном магнитном поле (∂В/∂t = 0). Здесь роль сторонних сил, разделявших разноименные заряды в проводнике, играет состав-ляющая силы Лоренца, направленная параллельно участкам (или одно-му участку) контура. Если неподвижный проводник находится в изме-няющемся со временем поле (∂В/∂t ≠ 0), то механизм возникновения э. д. с. оказывается другим. Изменяющееся магнитное поле возбуждает вих-ревое электрическое поле, под действием которого и происходит разде-ление разноименных носителей заряда в проводнике.
Токи Фуко.
Если объемный проводник поместить в изменяющееся во времени магнитное поле B(t), то в его объеме возникнут индукционные токи, которые будут течь по некоторым замкнутым траекториям, охваты-вающим линии В. Такие токи называются вихревыми токами или то-ками Фуко. Французский физик Л.Фуко впервые заметил,что сердеч-ники электрических машин нагреваются, если их пронизывает изменяющееся во времени магнитное поле.
Силу тока и распределение линий вихревых токов в объеме мас-сивного проводника рассчитать достаточно трудно. Плотность вихре-вых токов зависит от удельного сопротивления материала проводника и от скорости изменения внешнего магнитного поля.
Вихревые токи вызывают нагревание сердечников трансформато-ров и металлических частей электрических машин. Для снижения по-терь электрической энергии из-за возникновения вихревых токов сер-дечники трансформаторов изготавливают не из сплошного куска ферромагнетика, а из металлических пластин, отделенных друг от дру-га диэлектрической прослойкой. Причем плоскости пластин распола-гаются так, чтобы они были перпендикулярны направлению токов Фу-ко. Этот технический прием значительно повышает сопротивление сердечника по отношению к вихревым токам и, что очень важно, прак-тически не влияет на его магнитные свойства. Электрическое сопро-тивление сердечников повышается, если они изготовлены не из метал-лов, а из магнитодиэлектриков спрессованных под большим давлением смесей порошков ферромагнетиков и диэлектриков. Сердечники из ферритов (полупроводниковых ферромагнитных материалов)имеютудельное сопротивление, которое в миллиарды раз превышает удель-ное сопротивление обычных ферромагнитных веществ.
Если в проводнике, поперечное сечение которого не изменяется, протекает постоянный ток, то плотность тока одинакова в разных точ-ках сечения этого проводника. В случае переменного тока магнитное поле внутри проводника изменяется, и в нем возникают вихревые то-ки. Эти токи направлены так, что внутри проводника они противодей-ствуют, а вблизи поверхности проводника − способствуют изменению основного тока. Таким образом, в случае переменного тока сопротив-ление внутренней части проводника будет больше, чем внешней части. Плотность переменного тока максимальна у поверхности проводника и минимальна на его оси. Такое явление получило название скин-
эффекта(илиповерхностного эффекта).Для токов высокой частотыприменяют проводники трубчатой формы, так как внутренняя часть проводников не играет никакой роли.
Скин-эффект используется для поверхностной закалки различных деталей машин, т. к. при нагревании сплошных проводников токами высокой частоты практически вся теплота выделяется в поверхност-ном слое. При этом обеспечивается износостойкость детали.
Вихревые токи широко используются для плавки металлов в ин-дукционных печах. В этом случае они должны быть как можно боль-ше, так как согласно закону Джоуля − Ленца количество теплоты, вы-делившейся в проводнике R, пропорционально квадрату силы тока. Для увеличения вихревых токов в индукционных печах используются токи высокой частоты, которые создают быстро изменяющееся элек-тромагнитное поле, что в свою очередь приводит к увеличению инду-цированной ими ЭДС.
Дата добавления: 2017-01-08; просмотров: 2074;











