Энергия и объемная плотность энергии магнитного поля.
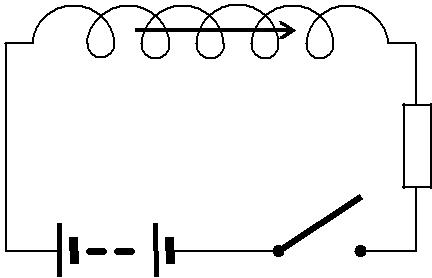
Рассмотрим электрическую цепь, изображенную на рис. 3.4.1. Пусть при включенной э. д. с. (ключ К в положении 1) в цепи те-
чет ток I, который создает в соленоиде магнитное поле В и сцеплен-ный с витками соленоида полный поток Ψc = LI.
Если ключ К перевести в положение 2, то магнитное поле начнет уменьшаться, поскольку в цепи некоторое время будет течь постепен-но убывающий ток, который поддерживается возникающей в соле-
ноиде ЭДС самоиндукции. Если считать индуктивность L = const, то э. д. с. равна:
| εc = −L dI . | (3.4.1) | ||
| dt | |||
| L | |||
| B | |||
| 2 | R | ||
| ε | К 1 | ||
| Рис. 3.4.1 |
Работа, совершаемая этим током за время dt, равна:
| δ A = εc I dt = −LIdI. | (3.4.2) |
Полную работу, которая совершается в цепи за время изменения силы тока от I до нуля, определим путем интегрирования элементар-ной работы δА:
| 1 | LI 2. | ||
| A = −∫ LIdI = | |||
| I | (3.4.3) |
Эта работа расходуется на изменение внутренней энергии сопротив-ления R, т. е. на его нагревание в соответствии с законом Джоуля – Ленца.
Совершение работы сопровождается исчезновением магнитного поля в соленоиде, поэтому естественно предположить, что она выпол-няется за счет энергии магнитного поля, сосредоточенного внутри со-леноида. Следовательно, в общем случае проводник с индуктивно-стью L, по которому проходит ток I, обладает энергией, равной энергии магнитного поля этого тока:
| Wm = | LI 2. | (3.4.4) | ||
Энергию магнитного поля можно выразить через величины, характе-ризующие поле: индукцию В поля и объем V, занимаемый этим полем.
Для соленоида L = μμ0n2V и B = μ0nI, поэтому энергия магнитного поля соленоида равна
| W | = | μμ | n 2VI 2 | = | B 2V = | HBV = | μμ | H 2V . | (3.4.5) | |||||
| m | 2μμ0 | |||||||||||||
Магнитное поле длинного соленоида практически однородно в его объеме. В связи с этим естественно предположить , что энергия магнитного поля В распределена равномерно с объемной плотностью
| wm = | dWm | = | B 2= | 1 HB = | 1 | μμ0H 2. | (3.4.6) | ||
| 2μμ0 | |||||||||
| dV |
Рассмотрим теперь неоднородное магнитное поле, когда В = В(х,у,z). В пределах бесконечно малого объема dV поле можно считать одно - родным, поэтому энергия dWm, заключенная в этом объеме dV, равна:
| dWm = wmdV. | (3.4.7) |
Интегрируя это выражение по объему V поля, мы можем опреде-лить полную энергию магнитного поля:
| Wm =∫wmdV . | (3.4.8) |
| V |
Дата добавления: 2017-01-08; просмотров: 2708;











