Второй (прямой) метод Ляпунова

Второй метод Ляпунова связан с физическими представлениями о равновесии материальной точки в консервативном силовом поле. Из физики известно, что точки минимума потенциальной энергии являются положениями устойчивого равновесия материальной точки (рис. 3.6, а), а точки максимума потенци альной энергии - положениями неустойчивого равновесия (рис. 3.6, б). Основная идея второго метода Ляпунова состоит в нахождении такой функции координат точки пространства со стояний системы V(η₁,...,η_n) , которая была бы до некоторой степени аналогична потенциальной энергии покоящейся материальной точки в обычном пространстве.

Введем некоторые определения.

Функция V(η₁,...,η_n) называется знакопостоянной, если она имеет один и тот же знак всюду в некоторой области, содержащей начало координат, за исключением некоторых точек, в которых она равна нулю.

Знакопостоянная функция, равная нулю лишь в начале координат, называется знакоопределенной : определенно - положительной или определенно - отрицательной, в зависимости от знака. Например, в трехмерном пространстве (n = 3) функция

V = а²η₁² + b²η₂² + c²η₃² является знакоопределенной функцией, а функция V = (η₁ + η₂)² + c²η₃² - знакопостоянной функцией, которая обращается в нуль на прямой η₂ = -η₁ и η₃ = 0
A.M. Ляпунов доказал следующие две теоремы.
Теорема 4.3. Если дифференциальные уравнения возмущенного движения таковы, что можно найти знакоопределенную функцию V, полная производная которой по времени

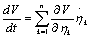(4.27)
в силу этих уравнении знакопостоянна и имеет знак, противоположный знаку функции V , или тождественно равна нулю, то невозмущенное движение устойчиво.
Доказательство теоремы. Выбираем произвольное достаточно малое ε > 0 и построим сферу

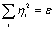(Рис. 4.12)

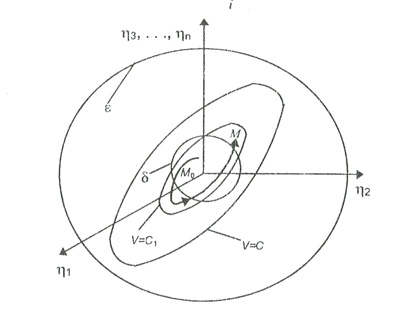
Рис. 4.12 - Устойчивость по Ляпунову

Затем построим поверхность V = С, лежащую внутри сферы ε. Это можно всегда сделать, так как функция V непрерывна и равна нулю в начале координат. Выбеоем теперь число δ настолько малым, чтобы сфера 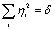целиком лежала внутри поверхности V = С, не имея с ней общих точек. Покажем, что изображающая точка М, начав движение из сферы δ никогда не дойдет до сферы ε, что и будет служить доказательством Устойчивости движения.
Не нарушая общности, можно считать, что функция V определенно-положительная (если V<0, то можно взять функцию минус V).

По условию теоремы ее производная, вычисленная в силу уравнений возмущенного движения, будет отрицательной или тождественно равной нулю функцией V≤0, т.е. функция V(η(t)) - невозрастающая функция. Тогда из соотношения 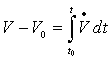, где V₀ - значение V в точке М₀, будем иметь V - V₀≤ 0, или V ≤ V₀. Отсюда следует, что при t≥t₀ изображающая точка М либо находится на поверхности V = V₀ = C₁ (при 0), либо внутри этой поверхности. Таким образом, изображающая точка М, начав движение из точки М₀ принадлежащей сфере δ, никогда не выйдет за пределы поверхности V = С₁, и тем более не сможет достичь сферы ε.
Приведем пример, иллюстрирующий теорему 4.3.
Пусть уравнения возмущенного движения имеют вид:

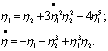
Возьмем определенно-положительную функцию

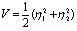
и вычислим ее производную по времени. В силу уравнений возмущенного движения имеем 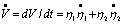. Подставляя вместо и их значения из уравнений возмущенного движения, получим

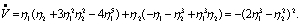
Так как функция V определенно-положительная, а ее производная 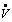отрицательная функция, то выполнены условия теоремы Ляпунова об устойчивости движения и, следовательно, невозмущенное движение η₁=0, ┧₂=0 устойчиво.
Теорема 4.4. Если дифференциальные уравнения возмущенного движения таковы, что можно найти знакоопределенную функцию V, полная производная которой по времени в силу этих уравнений знакоопределенна и имеет знак, противоположный знаку функции V, то невозмущенное движение асимптотически устойчиво.
Геометрическая иллюстрация теоремы Ляпунова об асимптотической устойчивости может быть представлена тем же рис.4.12, но с той разницей, что при V > 0 имеем < 0. При этом по свойству (4.27) фазовая траектория, пересекая поверхности V=const извне внутрь, не может оставаться на них, а пойдет внутрь до начала координат, η_i=0 (i=1,...,n) и V=0 . Ход аналитического доказательства теоремы 4.4 остается тем же, что и теоремы 4.3, но с изменением неравенств "≤" на " < ".
Функции V, удовлетворяющие условиям теорем 4.3, 4.4, называются функциями Ляпунова.
Второй (прямой) метод оценки устойчивости по Ляпунову дает достаточные условия устойчивости, т.е. движение системы может быть устойчивым и при невыполнении условий теорем 4.3, 4.4 Ляпунова.
Метод исследования устойчивости с помощью функции Ляпунова V(η₁,...,η_n) эффективен и применим к любым нелинейным системам, так как он не накладывает каких-либо ограничений на правые части уравнений движения системы. Однако практическое применение этого метода осложнено трудностью нахождения функции Ляпунова V(η₁,...,η_n). Общих рекомендаций по нахождению этой функции для произвольных систем не существует. A.M. Ляпунов указал один метод нахождения функции V для линейных систем.
Для иллюстрации идеи второго (прямого) метода Ляпунова рассмотрим простой пример. Пусть имеется система уравнений

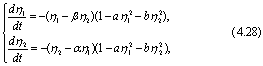
где 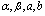- положительные постоянные коэффициенты.
Предложим для этой системы следующую функцию:

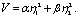(4.29)
Ее производная равна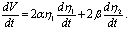
Подставив сюда выражение (4.28), получим

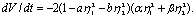
Производная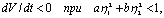
т.е. внутри эллипса 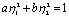движение устойчиво и фазовые траектории скручиваются к началу координат. Движение вне этого эллипса неустойчиво. Сам эллипс представляет собой неустойчивый предельный цикл.
Этот пример иллюстрирует редкий (счастливый) случай, когда не только находится функция Ляпунова, но и полностью определяется область, внутри которой состояние равновесия остается устойчивым.