Линеаризация непрерывных гладких нелинейных характеристик
Существует большой класс нелинейных систем, содержащих так называемые слабые нелинейности, имеющих непрерывные гладкие характеристики, которые при определенных допущениях можно линеаризовать, т.е. систему сделать линейной в математическом смысле. К настоящему времени известно 4 способа (методики) составления линеаризованных уравнений. Рассмотрим их последовательно.
Первый, аналитический способ линеаризации, называемый также методом малых отклонений, состоит в следующем:
1) определяется рабочая точка установившегося режима работы звена (х0,у0), в которой необходимо определить его поведение при малых отклонениях от установившегося режима (рис. 4.7);
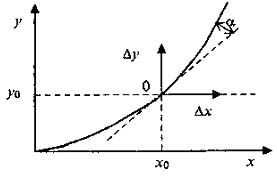
Рис. 4.7 - Линеаризация слабой нелинейности
2) нелинейная зависимость у = F(x) разлагается в ряд Тейлора в окрестности точки (х0,у0), в этом разложении отбрасываются члены выше первого порядка малости и получается следующая приближенная зависимость 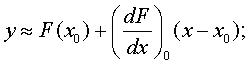
3) полученное приближенное уравнение переписывается в виде 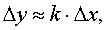
(4.9)
где 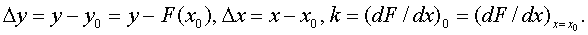
Часто в уравнениях вида (4.9) знак ∆ опускают и рассматривают линеаризованное уравнение в малых отклонениях, или, как еще говорят, в вариациях:
y = k•x. (4.10)
Рассмотрим в изложенной последовательности более общий случай, когда звено (система) описывается нелинейным уравнением вида
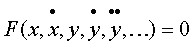 (4.11)
(4.11)
Разлагая, как и прежде, нелинейную функцию в ряд Тейлора в
точке установившегося режима, получим
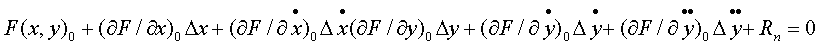 (4.12)
(4.12)
или
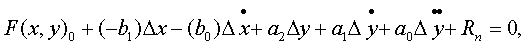
где Rn - остаточный член, определяющий члены порядка малости п≥2.
Из уравнения (4.12) вычтем уравнение (4.11) для установившегося режима работы САУ, т.е. вычтем F(x0,0,y0,0,0,...) = 0, и, опуская знак ∆ и отбрасывая Rn, получим линеаризованное дифференциальное уравнение динамики звена в малых отклонениях в виде (2.36) или операторной форме (2.37).
Допустимость такой линеаризации ограничена следующими условиями:
- она применима только к непрерывным дифференцируемым нелинейностям;
- она применима только для малых отклонений, т.е. полученные линеаризованные уравнения пригодны для приближенного исследования таких режимов работы системы, при которых переменные величины на ее входе имеют достаточно малые отклонения от установившихся значений, при этом точность исследования растет с уменьшением величины отклонений.
По второму, графическому способу линеаризация осуществляется на основе уравнений (4.10), (2.36) без проведения предварительных выкладок, с использованием графического смысла линеаризации. Суть состоит в замене кривой искомого решения нелинейных уравнений (4.1), (4.11) прямой, касательной к искомой кривой в точке (x0, у0), соответствующей начальным условиям. Угол, составленный этой касательной и осью абсцисс, будет равен 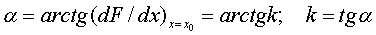 (рис. 4.7). Очевидно, что такая замена справедлива только для тех отклонений ∆х, при которых кривая незначительно отклоняется от касательной. Допустимая область отклонений и определяет возможности линеаризации нелинейной системы, при этом вместо частных производных находят частные разности.
(рис. 4.7). Очевидно, что такая замена справедлива только для тех отклонений ∆х, при которых кривая незначительно отклоняется от касательной. Допустимая область отклонений и определяет возможности линеаризации нелинейной системы, при этом вместо частных производных находят частные разности.
Для уравнений (4.10) и (2.36), записанных в отклонениях, графически это означает перенос начала координат в точку 0(x0,y0). Для реальных систем результат подобной линеаризации часто справедлив для достаточно больших значений отклонений; чем больше значения этих отклонений, тем больше к данным системам применим термин "линейная система" и тем больше степень достоверности результатов исследования САУ, полученных с помощью теории линейных систем.
Третий способ объединяет рассмотренные выше способы и предлагает сразу записывать уравнения линеаризуемого звена (системы) в отклонениях.
Четвертый способ линеаризации основан на использовании метода наименьших квадратов для определения коэффициентов уравнений (4.10) и (2.36).
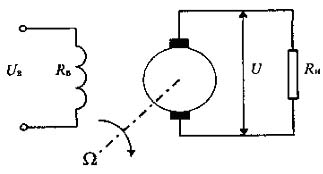
Рис 4.8 - Схема генератора постоянного тока
Рассмотрим в качестве примера вывод линеаризованного уравнения генератора постоянного тока (рис. 4.8). Такой генератор может входить в состав САУ, приведенной на рис. 2.3, в качестве электромашинного усилителя мощности.
Входной величиной генератора является напряжение возбуждения UB, а выходной - напряжение на его выходных зажимах U. Скорость вращения якоря Ω и величину сопротивления нагрузки RH будем считать постоянными. Реакция якоря предполагается скомпенсированной и не учитывается.
Напряжение генератора равно
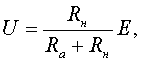
где Е - э.д.с. генератора; Ra - сопротивление цепи якоря генератора; RH - сопротивление нагрузки.
Э.д.с. генератора пропорциональна скорости вращения якоря и магнитному потоку, т.е.
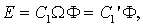
где Ω - угловая скорость вращения якоря; Ф - взаимодействующая с якорем часть магнитного потока, создаваемого обмоткой возбуждения; С1 - коэффициент, постоянный для данной машины.
Поток Ф является функцией тока возбуждения, т.е.
Ф = F(IB). (4.13)
Эта зависимость нелинейна (рис. 4.9).
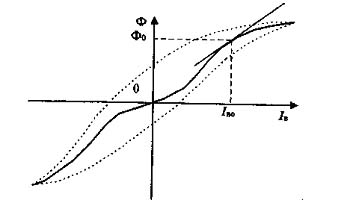
Рис. 4.9 - Нелинейная функция тока генератора
В свою очередь, напряжение возбуждения Uв зависит от тока возбуждения: Uв = 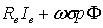 , где Iв - ток возбуждения; Rв- сопротивление цепи возбуждения; σ - число витков обмотки возбуждения; - коэффициент рассеяния магнитного потока, с помощью которого полный поток, создаваемый обмоткой возбуждения, выражается в виде σФ ( σ > 1). Таким образом, полученные четыре уравнения в совокупности определяют искомую зависимость U от Uв через промежуточные переменные Е, Ф и Iв. Эта зависимость нелинейна из-за нелинейности характеристики намагничивания генератора (4.13) и обусловлена насыщением магнитной цепи, а также гистерезисом. Петля гистерезиса (рис. 4.9) узка, ею можно пренебречь и ограничиться основной кривой намагничивания, показанной на рис. 4.9 сплошной линией. Переходя в уравнениях к приращениям переменных, получим следующую систему линейных уравнений:
, где Iв - ток возбуждения; Rв- сопротивление цепи возбуждения; σ - число витков обмотки возбуждения; - коэффициент рассеяния магнитного потока, с помощью которого полный поток, создаваемый обмоткой возбуждения, выражается в виде σФ ( σ > 1). Таким образом, полученные четыре уравнения в совокупности определяют искомую зависимость U от Uв через промежуточные переменные Е, Ф и Iв. Эта зависимость нелинейна из-за нелинейности характеристики намагничивания генератора (4.13) и обусловлена насыщением магнитной цепи, а также гистерезисом. Петля гистерезиса (рис. 4.9) узка, ею можно пренебречь и ограничиться основной кривой намагничивания, показанной на рис. 4.9 сплошной линией. Переходя в уравнениях к приращениям переменных, получим следующую систему линейных уравнений:
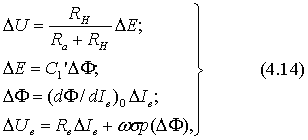
где (dФ/dIв)0 определяется как тангенс угла наклона касательной к основной кривой намагничивания в точке установившегося режима (рис. 4.9).
Исключив из системы (4.14) промежуточные переменные ∆Е, ∆Ф и ∆Iв получим искомое линеаризованное уравнение, связывающее ∆U с ∆Uв:
(Tвp+1) ∆U=kв1∆Uв, (4.15)
где Тв - постоянная времени цепи возбуждения:
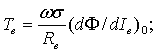
kв1 - коэффициент передачи генератора по возбуждению:
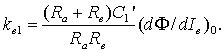
Заметим, что Тв и kв1 зависят от выбранной точки установившегося режима, в которой осуществляется линеаризация.
Если перейти к относительным единицам, то линеаризованное уравнение (4.15) примет следующий вид:
(Tвp +1)u = kв2Uв, (4.16)
где u=∆U/Uв; Uв=∆Uв/Uв0; kв2=kв1Uв0/Uв.
С использованием оператора передаточной функции получим следующее выражение:
u=Wв(p)Uв, (4.17)
где 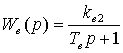
В заключение отметим, что при выводе уравнений (4.16), (4.17) скорость вращения якоря и сопротивление нагрузки были приняты постоянными. Если учесть их непостоянство, то в правой части этих уравнений появятся дополнительно второй и третий члены.
Изложенные выше способы линеаризации относительно рабочей точки установившегося режима или положения равновесия нелинейной системы можно без труда обобщить, проводя линеаризацию относительно некоторого решения или траектории движения системы. Этот прием успешно применяется, например, в задачах космической навигации, когда известна расчетная траектория движения объекта (космического корабля). После линеаризации исходных уравнений оказывается возможным определить управляющие воздействия, которые будут удерживать космический корабль вблизи расчетной траектории.
Анализируя полученные линеаризованные уравнения, можно оценить влияние ошибок при задании начальных условий и параметров объекта, определить функции чувствительности.
Полученные при линеаризации линейные уравнения, как правило, нестационарны, а имеющиеся теоретические результаты исследования линейных систем (см. раздел 3) относятся в основном к стационарным линейным системам.
Для нестационарных систем теория, с одной стороны, находится в стадии разработки, а с другой - сложна в приложениях. И самое главное, в случае нестационарной системы следует постоянно помнить о степени малости и задавать себе вопрос, достаточно ли малы изменения переменных и остаются ли они в области, где линеаризованные уравнения справедливы.
Если имеются сомнения, то решения линеаризованного уравнения должны постоянно сравниваться с численным решением исходного нелинейного уравнения.
Если линеаризованные уравнения адекватны решаемой нелинейной задаче, то их полное решение может быть легко выписано, а изложенные в разделах 2 и 3 методики удобны для их исследования.
Ситуация совсем иная, если дифференциальные уравнения звеньев, а значит и системы в целом, не линеаризуются переходом к малым колебаниям около положения исследуемого равновесия. Не только общее решение, но даже поиск периодических решений является сложной и не всегда преодолеваемой до искомого решения задачей. Теория нелинейных САУ создавалась путем постепенного преодоления этих трудностей.
Устойчивость нелинейных систем
Понятие устойчивости естественно и просто введено в подразделе 3.2 для линейных систем. Там же сформулированы необходимые и достаточные условия устойчивости. Для стационарных линейных систем единственным положением равновесия будет начало координат, если выполнено два условия: характеристическое уравнение системы не имеет полюсов с действительной частью, а входной сигнал равен нулю. На этой основе определены два эквивалентных условия устойчивости (или неустойчивости) положения равновесия (начала координат) системы.
1. Система устойчива (или неустойчива) при отсутствии входного сигнала, если при произвольных начальных условиях фазовые траектории стремятся к началу координат (или уходят в бесконечность).
2. Система устойчива (или неустойчива) при ограниченном входном сигнале, если выходной сигнал ограничен (или неограничен).
Первое условие определяет поведение свободной системы в переходном процессе, а второе - поведение системы при неравном нулю входном сигнале. Оба условия устойчивости эквивалентны для стационарных линейных систем.
В нелинейных системах нет такой простой связи между этими двумя типами устойчивости, так как свободное движение системы может существенно отличаться от вынужденного.
Рассмотрим в качестве примера нелинейную систему первого порядка, описываемую уравнением вида 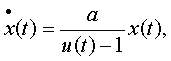 где а > 0.При u(t) ≡ О система устойчива, но при u(t) ≠ О всякий раз, когда управление u(t)=1, x(t)→∞ ; если u(t) = const > 1, то реакция системы также не ограничена. Следовательно, нельзя гарантировать ограниченность реакции при ограниченном управлении, т.е. в рамках второго определения вопрос об устойчивости нелинейной системы не решается.
где а > 0.При u(t) ≡ О система устойчива, но при u(t) ≠ О всякий раз, когда управление u(t)=1, x(t)→∞ ; если u(t) = const > 1, то реакция системы также не ограничена. Следовательно, нельзя гарантировать ограниченность реакции при ограниченном управлении, т.е. в рамках второго определения вопрос об устойчивости нелинейной системы не решается.
В этой связи анализ устойчивости нелинейных систем проводится в рамках первого определения. Однако для нелинейных систем вопрос об устойчивости значительно сложнее. При исследовании нелинейных систем используются понятия устойчивости в малом, в большом, в целом, абсолютная устойчивость:
- устойчивость в малом - это устойчивость при бесконечно малых отклонениях относительно исходного режима (положения равновесия);
- устойчивость в большом - это устойчивость при конечных отклонениях относительно положения равновесия, возможных в данной системе по условиям ее работы;
- устойчивость в целом - это устойчивость при любых отклонениях от исходного режима, т.е. при отсутствии каких-либо ограничений (при любых начальных условиях);
- абсолютная устойчивость - это асимптотическая устойчивость системы в целом при любом характере нелинейности внутри определенного класса нелинейностей.
Поясним на примере трудности анализа нелинейных систем. Пусть поведение системы описывается уравнением Ван-дер-Поля:
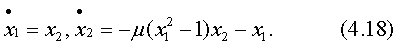
Решение этого уравнения для μ=0,2 представим в виде
фазовых траекторий на фазовой плоскости 0х1x2 (рис. 4.10).
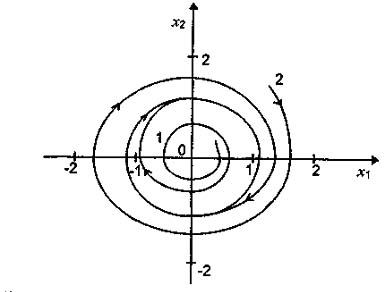
Рис. 4.10 - Фазовый портрет для системы (4.18)
Поясним использованные термины.
Фазовое пространство. Текущие значения координат x1,x2,...,xn нелинейной системы удобно представлять в виде точки в n-мерном декартовом пространстве, называемом пространством состояний или фазовым пространством системы. Дифференциальные уравнения системы, записанные в нормальной форме (2.42), определяют значения проекций вектора скорости, с которой будет перемещаться данная точка фазового пространства.
фазовые траектории. Точка фазового пространства, соответствующая состоянию системы в данный момент времени, называется изображающей точкой. Геометрическое место изображающих точек, соответствующее последовательному изменению состояния системы со временем в фазовом пространстве, называется фазовой траекторией или интегральной кривой. Полная совокупность интегральных кривых, соответствующая всем возможным начальным условиям, называется фазовым портретом системы.
Фазовая плоскость. Фазовая плоскость является частным случаем фазового пространства и используется для исследования нелинейных систем, описываемых уравнениями первого и второго порядков. Если
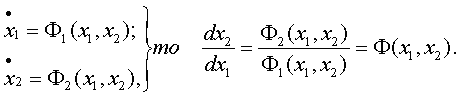
Это уравнение фазовой траектории - интегральной кривой на фазовой плоскости.
Вблизи начала координат (рис. 4.10) фазовые траектории 1 раскручиваются и стремятся к замкнутой траектории (предельному циклу). Фазовые траектории 2, начинающиеся вне предельного цикла, также со временем сходятся к нему. Следовательно, система, описываемая уравнением (4.18), неустойчива в "малом" относительно положения равновесия, но при этом всякое движение со временем переходит в предельный цикл. Если амплитуда предельного цикла оказывается малой, то такое поведение системы при больших сигналах оказывается приемлемым, т.е. система, неустойчивая при малых отклонениях от положения равновесия, практически устойчива при значительных отклонениях.
Подведем предварительные итоги изложенных выше рассуждений:
- в отличие от линейных систем для нелинейных систем следует говорить об устойчивости относительно положения равновесия, а не об устойчивости системы вообще;
- устойчивость в малом еще не определяет устойчивость во всем фазовом пространстве (пространстве состояний системы), и эти две задачи следует изучать раздельно;
- даже при анализе устойчивости в малом следует рассматривать два случая: либо все фазовые траектории системы никогда не покидают некоторой определенной окрестности положения равновесия, либо все траектории асимптотически приближаются к рассматриваемому положению равновесия.
Впервые свойства устойчивости в изложенном выше понимании были исследованы русским ученым A.M. Ляпуновым в 1892 г. в работе "Общая задача об устойчивости движения".
Дата добавления: 2021-04-21; просмотров: 698;











