Устойчивость в малом (устойчивость по Ляпунову)

Запишем уравнения динамики системы n-го порядка в общем нелинейном виде в нормальной форме Коши:
dx_n/dt = F_k(x₁,x₂,...,x_n,t), k = 1,2,...,n, (4.19)
где x₁,x₂,...,x_n - величины, определяющие состояние системы в каждый данный момент времени;
F_k - некоторые нелинейные функции.
Заметим, что в частном случае линейной системы уравнения (4.19) перепишутся в форме (2.42).
Наличие t под знаком функции F_k(k = 1,2,...,п) объясняется либо тем, что на систему действуют изменяющиеся во времени внешние воздействия, либо тем, что некоторые параметры системы изменяются во времени. Системы, описываемые уравнениями вида (4.19), с правыми частями, зависящими только от величин x₁,x₂,...,x_n и не зависящими явно от времени t, называются автономными.
Будем считать, что функции F_k(k=1,2,...,n) таковы, что при заданной совокупности начальных условий x_k(t₀) = x_k0 (k=1,2,...,n), t=t₀ - произвольный момент времени, принимаемый за начальный, существует единственное решение системы уравнений (4.19). Из совокупности возможных решений системы уравнений (4.19) выберем одно x_k=x*_k(t) (k=1,2,...,n), отвечающее определенным начальным условиям, которое назовем невозмущенным движением системы. Всякое другое движение, отличное от невозмущенного (соответствующее другим начальным условиям), будем называть возмущенным.
Выбор невозмущенного движения произволен. Обычно невозмущенным движением называют такое, которое инженер принимает за расчетное движение системы. От этого движения систему отклоняют различные возмущения. Сформулируем определение устойчивости по A.M. Ляпунову.
Невозмущенное движение называется устойчивым по Ляпунову, если для всякого ε > 0 можно указать δ > 0 такое, что из неравенства

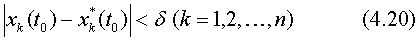
следует при всех t≥t₀ неравенство
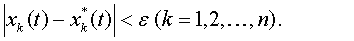(4.21)
Невозмущенное движение x*_k(t) называется асимптотически устойчивым по Ляпунову, если оно устойчиво в смысле Ляпунова и если существует такое положительное h, что при 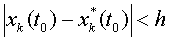будем иметь
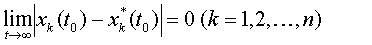(4.22)
Если существует хотя бы одно такое число ε > 0, что при любом сколь угодно малом δ > 0 существует возмущенное движение, удовлетворяющее условию (4.20), для которого при некоторых значениях t>t₀неравенства (4.21) не выполняются, то невозмущенное движение называется неустойчивым.
Этим определениям можно дать геометрическую интерпретацию. Будем изображать отклонение возмущенного движения системы от невозмущенного в каждый момент времени t точкой n-мерного пространства с прямоугольными декартовыми координатами

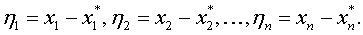
На рис. 4.11 представлена геометрическая интерпретация определений устойчивости по A.M. Ляпунову. Заметим, что в приведенных выше аналитических определениях области ε и δ, в отличие от рис. 4.11, выглядят гиперкубическими (в n-мерном пространстве), но это не имеет принципиального значения.
Невозмущенное движение (в данном случае начало координат) устойчиво (рис. 4.11. а), если при любом как угодно малом радиусе ε сферы С_ε существует такая сфера С_δ радиусом δ, что изображающая точка не может выйти за пределы сферы С_ε, начав движение из любой точки сферы С_δ.

Невозмущенное движение асимптотически устойчива (рис. 4.11, б), если существует такая сфера С_δ, что изображаю, щая точка стремится к началу координат, начав движение из лю-бой точки сферы С_δ.

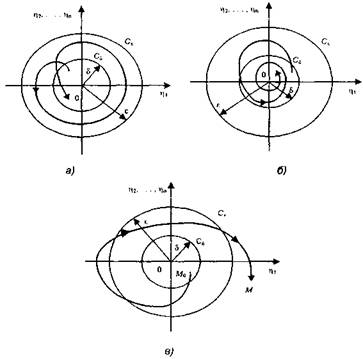
Рис. 4.11 - Устойчивость по Ляпонову

Невозмущенное движение неустойчиво (рис. 4.11, в), если существует такая сфера С_ε и как угодно близко к началу коор-динат можно найти такую точку М_o, что изображающая точка М выйдет за пределы сферы С_ε, начав движение из точки М_o.
В определении устойчивости по Ляпунову невозмущенное и возмущенное движения рассматриваются всегда при одних и тех же входных сигналах системы, представляющих собой вполне определенные функции времени. Поэтому одна и та же система при одних и тех же начальных условиях невозмущенного движения t_o,x*₁₀,...,x*_n0 может быть устойчивой по Ляпунову при одних входных сигналах и неустойчивой при других входных сигналах.
Межде тем в задачах практики приходится оценивать устойчивость работы системы при различных заранее неизвестных входных сигналах, что делает определение устойчивости по Ляпунову недостаточным для практики.
Приведем еще одно определение устойчивости, учитывающее изменение как начальных условий, так и входного сигнала, т.е. оба условия устойчивости, эквивалентных для линей-ных систем и сформулированных в самом начале настоящего подраздела.
Будем считать, что при изменении формы входных сигналов правые части дифференциальных уравнений (4.1) изменяются непрерывно, т.е. при замене входных сигналов достаточно близ-кими к ним другими входными сигналами функции F_k в уравнениях (4.19) изменяются сколь угодно мало. В этом случае дифференциальные уравнения возмущенных движений можно написать в виде
x_k=F_k(x₁,...x₁,t) + φ_k(x₁,...x_n,t)t (k = l,2,...,n), (4.23) где φ_k - функции, сколь угодно малые по абсолютной величине при любых достаточно малых отклонениях входных сигналов системы от входных сигналов, соответствующих невозмущенному движению.
Различным входным сигналам системы соответствуют различные функции φ_k в уравнениях (4.23). В частности, φ_k =0 для невозмущенного движения.
Назовем невозмущенное движение системы устойчивым, если отклонение ее возмущенного движения от невозмущенного остается сколь угодно малым при любых достаточно малых начальных отклонениях и при любых входных сигналах, достаточно близких к входным сигналам, соответствующим невозмущенному движению. В аналитической форме это определение понятия устойчивости формулируется следующим образом.
Невозмущенное движение системы называется устойчивым, если при сколь угодно малом ε > 0 существуют такие числа δ = δ(ε) и δ' = δ'(ε) , что для всех возмущенных движений, Удовлетворяющих условию (4.20), при любом t > t₀ выполняются неравенства (4.21), если |φk,(x*₁,...,x*_n,t)|<δ' (к = 1,2,...,n).
Доказано, что при довольно общих условиях невозмущенное движение системы устойчиво в смысле данного определения, если оно асимптотически устойчиво по Ляпунову, т.е. исследование устойчивости нелинейной системы практически сводится к исследованию ее асимптотической устойчивости. Имен-но этим объясняется большое практическое значение теории устойчивости движения, созданной A.M. Ляпуновым.