Аппроксимация, устойчивость и сходимость

Разностных схем

Важный вопрос, относящийся к численным решениям, состоит в том, до какой степени мы можем гарантировать, что численное решение дифференциального уравнения в частных производных будет близко к точному решению, а также при каких условиях это численное решение совпадает с точным? Очевидный ответ на вторую часть этого вопроса состоит в том, что следует требовать, чтобы приближенное (численное) решение сходилось к точному решению, если размеры ячеек сетки стремятся к нулю. Однако сходимость очень трудно установить таким прямым путем. Поэтому обычно используют обходной путь, который связан с требованием о том, чтобы система алгебраических уравнений, полученная в результате процесса дискретизации, была согласованной с исходным дифференциальным уравнением в частных производных.

Согласованность означает, что с помощью разложения в ряд Тейлора, процесс дискретизации может бытьобращен с целью восстановления исходного дифференциального уравнения. Кроме того, алгоритм, который служит для решения алгебраических уравнений, должен быть устойчивым.

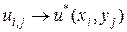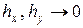Решение алгебраических уравнений, аппроксимирующих заданное дифференциальное уравнение, называется сходящимся, если это приближенное (численное) решение приближается к точному решению дифференциального уравнения для любого значения независимой переменной, по мере того как размеры ячеек сетки приближаются к нулю. Например, для функции двух переменных можно записать: при , где 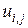– решение разностного уравнения, 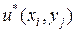– точное решение дифференциального уравнения в узлах сетки. Точное решение системы алгебраических уравнений 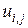является приближенным решением для исходного дифференциального уравнения, отклонение 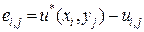называется ошибкой решения в узловой точке .

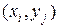Сходимость решения разностной схемы (системы алгебраических уравнений) к решению исходного дифференциального уравнения проверяется по выражению 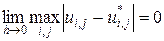, где 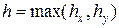. Если при этом справедлива оценка 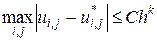, то имеет место сходимость порядка 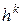(разностная схема имеет 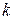-й порядок точности относительно 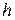), постоянные 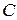и 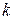не зависят от .

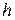На следующем рисунке изображена концептуальная связь между согласованностью, устойчивостью и сходимостью.

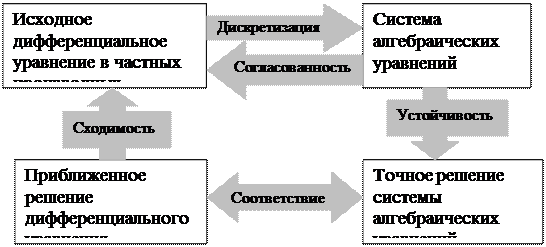
Обычно сходимость устанавливают численными расчетами при различных размерах ячейки сетки. Сходимость приближенного решения метода конечных разностей к точному решению дифференциального уравнения тесно связана с понятием согласованности системы алгебраических уравнений, полученных в результате процесса дискретизации, с исходным дифференциальным уравнением и устойчивостью метода решения полученной системы алгебраических уравнений.

Говорят, что система алгебраических уравнений, полученная в результате процесса дискретизации, согласуетсяс первоначальным дифференциальным уравнением, если в пределе, когда размеры ячеек сетки стремятся к нулю, система алгебраических уравнений эквивалентна дифференциальному уравнению в каждой из узловых точек сетки. Условие согласованности не является достаточным для сходимости, но является необходимым.

Понятие устойчивости связано с ростом или затуханием ошибок, вносимых в расчет на любом его этапе, особенно ошибок округления, т.к. в расчетах на ЭВМ используется конечное число значащих цифр. Конкретный метод считается устойчивым, если кумулятивный эффект всех ошибок округления, возникших в процессе применения данного алгоритма, является пренебрежимо малым. Двумя наиболее общеупотребительными методами анализа устойчивости являются матричный метод и метод Неймана[8,50]. В основе обоих методов лежит возможность предсказания, будет ли иметь место рост ошибки как разности, учитывающей погрешности округления.

Обсуждение проблем сходимости, согласованности и устойчивости касалось поведения приближенного решения в пределе при 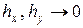. Однако на практике приближенные решения строятся на сетке конечных размеров и соответствующая точность имеет немаловажное значение. Один из путей определения точности конкретного алгоритма на сетке конечных размеров состоит в том, чтобы применить этот алгоритм к решению родственной, но более простой задачи, имеющей точное решение. Однако, тот алгоритм, который был достаточно точным для модельной задачи, необязательно будет столь же точным для первоначальной задачи.

Другой способ оценки точности состоит в том, чтобы строить решения на последовательно измельчаемых сетках и проверять, будет ли при таком последовательном измельчении решение изменяться в рамках заранее предопределенной степени точности. Также численные решения полезно сравнить с надежными экспериментальными результатами той же самой задачи.

Можно ожидать, что в некоторых специальных случаях применение схем высокого порядка или использование мелких сеток могут привести к построению более точных решений, но еще важно время счета. Следовательно, вычислительную эффективность можно определить как точность, достигаемую в расчете на единицу времени исполнения.

Область применения численных методов в настоящее время стремительно расширяется, рассматриваемые при этом математические модели в большинстве случаев описываются при помощи линейных и нелинейных уравнений в частных производных математической физики. Поскольку каждому дифференциальному уравнению можно поставить в соответствие множество разностных аппроксимаций (схем), а для численного решения появившихся при этом разностных уравнений – ряд методов их решения, возникает проблема выбора одной схемы и одного вычислительного алгоритма на ЭВМ. Критерием выбора конкретной схемы и вычислительного алгоритма для ЭВМ часто рассматривают экономичность алгоритма, так как, в конечном счете, алгоритм должен дать решение исходной задачи с любой заданной точностью за минимальное число операций на ЭВМ. При теоретических оценках экономичность алгоритма часто заменяется требованием минимума арифметических действий, достаточных для получения решения с заданной точностью.

Для численного решения уравнений в частных производных могут применяться различные методы, например, метод конечных разностей (метод сеток), вариационные методы (метод Ритца), метод конечных элементов. [