Первый метод Ляпунова

Первый метод Ляпунова основан на линеаризации уравнений, описывающих поведение системы.
Линеаризация осуществляется разложением всех входящих в уравнение (4.19) функций F_k(k = 1,2,...,л) в ряд Тейлора и отбрасыванием всех членов выше первой степени относительно величин η₁ = x₁ - х*₁; η₂ = х₂ - х*₂,...; η_n = x_n - х*_n , т.е.
F_k(x₁,...,x_n,t) ≈ F_k(x*₁,...,x*_nt) + 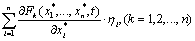(4.24)

Подставляя (4.24) в (4.19) и учитывая, что невозмущенное движение удовлетворяет (4.19), т.е. x*_k=F_k(x*₁,...,x*_n,t), (к=1,...,n), получим систему линейных дифференциальных уравнений относительно η₁,η₂,...,η_n
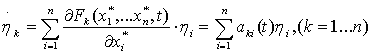(4.25)

величины η₁,η₂,...,η_n определяют отклонение возмущенного движения от невозмущенного. Их принято называть вариациями переменных x₁,x₂,...,x_n, определяющих состояние системы. Приближенные линейные уравнения (4.25) называются уравнениями в вариациях или линейными уравнениями первого приближения.
Приведем без доказательства теоремы A.M. Ляпунова, справедливые для автономных систем, для которых a_ki(t) = a_ki - const, а характеристическое уравнение первого приближения определяется выражением (2.43).
Теорема 4.1. Если вещественные части всех корней характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво независимо от членов разложения выше первого порядка малости.
Теорема 4.2. Если среди корней характеристического уравнения первого приближения найдется по меньшей мере один с
положительной вещественной частью, то невозмущенное движение неустойчиво независимо от членов разложения выше первого порядка малости.
Данные теоремы позволяют однозначно разрешить вопрос об устойчивости (или неустойчивости) невозмущенного движения автономной нелинейной системы на основании исследования уравнений первого приближения только для структуры корней характеристического уравнения, указанной в условиях теорем. Если структура корней характеристического уравнения другая, то для определения характера устойчивости одних уравнений первого приближения недостаточно и необходимо рассмотреть влияние членов второго и высшего порядка малости, т.е. нужно оценивать устойчивость движения исходной системы уже по исходным уравнениям (4.19).
В общем случае, когда коэффициенты a_ki(t) уравнений
(4.25) являются любыми функциями времени, для исследования устойчивости движения можно применить общее необходимое и достаточное условие устойчивости линейной системы (3.38). Для этого необходимо определить весовые (импульсные переходные) функции ω_ij(t,τ) линеаризованной системы, описываемой уравнениями в вариациях (4.25), соответствующие всем входам (j=1,...,m) системы и всем переменным x_i(i = 1,...,n), и вычислить для них интегралы вида
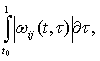(i=1,...,n; j=1,...,m) (4.26)

Выполнив эти вычисления для различных моментов времени t, можно судить об устойчивости системы. Если интегралы (4.26) для весовых (импульсных переходных) функций, соответствующих всем входам системы и всем переменным x₁,...,х_n;, перестают заметно изменяться с увеличением t , начиная с некоторого момента, то исследуемое невозмущенное движение нелинейной системы устойчиво по отношению к переменным x₁,...,х_n. Если же хотя бы один из интегралов (4.26) неограниченно возрастает с увеличением t , то невозмущенное движение нелинейной системы неустойчиво. Изложенный способ исследования устойчивости основан на пракгике анализа и моделирования реальных систем и не позволяет делать строгие выводы об Устойчивости или неустойчивости из-за невозможности осуществить путем расчетов на ЭВМ бесконечные процессы, связанные с предельным переходом в формуле (3.38).

Однако на практике такой способ исследования устойчи вости позволяет безошибочно судить об устойчивости невозмущенного (расчетного) движения нелинейной системы в течение любых интересующих исследователя интервалов времени.
В заключение еще раз подчеркнем, что изложенный метод исследования устойчивости нелинейных систем, основанный на линеаризации уравнений, описывающих поведение системы, применим лишь к системам, содержащим только элементарные нелинейные звенья с непрерывными гладкими характеристиками. К системам с существенными нелинейностями этот метод не применим. В таких случаях оказывается полезным следующий, второй метод Ляпунова.