Свойства нечетких бинарных отношений

Рассмотрим ряд важных свойств нечетких бинарных отношений [42]. Так же как и ранее будем полагать, что E₁×E₂ = E, то есть отношения задаются на одном и том же универсальном множестве.

Симметричность

Нечеткое бинарное отношение называется симметричным, если

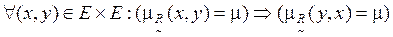. (4.6)

Для симметричного бинарного отношения значения функции принадлежности в ячейках таблицы, симметричных относительно ее главной диагонали, одинаковы (табл. 4.12).

Таблица 4.12

Симметричное нечеткое бинарное отношение

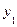
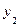
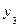
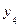
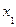
	0,2	0,3	0,4
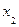
	0,3	0,4	0,6	0,5
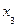
	0,4	0,6
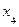
		0,5

Рефлексивность

Нечеткое бинарное отношение называется рефлексивным, если

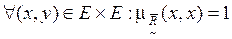. (4.7)

Из данного определения следует, что в ячейках на главной диагонали (таблица 4.13), представляющей это отношение, должны быть только 1.

Таблица 4.13

Рефлексивное нечеткое бинарное отношение

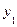
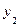
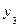
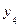
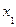
		0,6	0,2
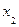
			0,3	0,7
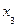
	0,4	0,3
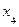
		0,2	0,5

Транзитивность

Нечеткое бинарное отношение называется транзитивным (табл. 4.14), если

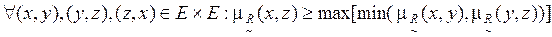. (4.8)

Таблица 4.14

Транзитивное нечеткое бинарное отношение

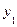
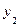
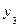
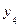
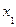
	0,2		0,4	0,4
		0,6	0,3
			0,3
	0,1			0,1

Антисимметричность

Нечеткое бинарное отношение называется антисимметричным, если (табл. 4.15).

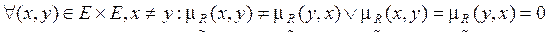. (4.9)

Таблица 4.15

Антисимметричное нечеткое бинарное отношение

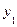
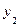
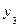
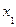
			0,7
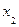
		0,4	0,6
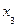
	0,8	0,3	0,2