Измененные значения исходного обучающего универсума
| Номер эксперта | k1 | k2 | k3 | k4 | k5 | k6 | H | H |
| x1 | ||||||||
| x2 | ? | |||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 | ||||||||
| x9 | ? | |||||||
| x10 |
Как и в предыдущем примере, выделим классы эквивалентности на основе значений классификационных атрибутов и атрибута класса:
IND(X) = {{xl, x5}, {x2, x6, x8}, {x3}, {x4, x9}, {x7, x10}}; (4.32)
X1= {xl, x5}; X2 = {x2, x6, x8}; X3 = {x3}; X4 = {x4, x9}; X5 = {x7, x10}.
IND(H) = {xl, x4, x5},{x2, x3, x6, x7, x8, x9 , x10}}. (4.33)
H1 = {xl, x4, x5}, H2 = {x2, x3, x6, x7, x8, x9 , x10}.
Отсюда очевидно, что в данном примере невозможно выделить классы эквивалентности в IND(H), как объединения некоторых классов эквивалентности в IND(X), что в свою очередь, не дает возможности корректно классифицировать все примеры обучающего универсума. Для представления подмножеств обучающего универсума с позиций ТГМ определим нижние и верхние аппроксимации атрибута классов 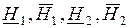 а также их отрицательную (NEG), положительную (POS) и граничную (BN)области:
а также их отрицательную (NEG), положительную (POS) и граничную (BN)области:
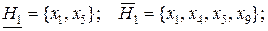
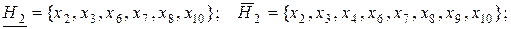
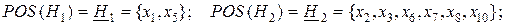
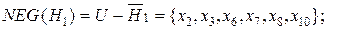 (4.34)
(4.34)
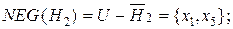
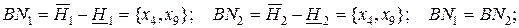
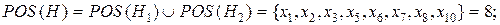
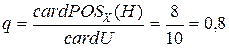 .
.
Таким образом, 8 примеров из 10, представленных в таблице 4.21 классифицируются корректно, используя подход грубых множеств.
Изменим еще раз условия примера введением еще одной колонки H* в табл. 4.21, где значения х2 и х9 обозначены знаком вопроса (?). Данные значения образуют область незнания, т.е. нельзя сказать, к какому из классов они относятся.
С учетом этого, вид выражения для IND(X) останется таким же, как в 4.32, что же касается IND(H), то оно примет следующий вид:
IND(H) = {{Hl},{H2}, {H?}}.
Hl = {xl, x4, x5}; H2 = {x3, x6, x7, x8, x10}; H? = {x2, x9}
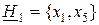 ;
; 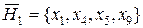 ; (4.35)
; (4.35)
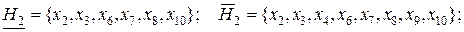
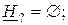
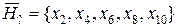 .
.
Поскольку 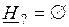 , принципиально нельзя сделать выводы о потенциальной принадлежности х2 и х9 к одному из классов, используя информацию о значениях классификационных атрибутов.
, принципиально нельзя сделать выводы о потенциальной принадлежности х2 и х9 к одному из классов, используя информацию о значениях классификационных атрибутов.
Поэтому целесообразно рассмотреть вопрос о том, влияет ли отсутствие информации о классах х2 и х9 на общие результаты классификации значений исходного обучающего универсума U.
Для этого можно условно назначить принадлежность х2 и х9 к любому из классов, или к обоим классам, и проверить, как изменится граничная область BN.
Включим, например, эти значения в класс H1 т.е. H1 = {x1, x2, x4, x5, x9}.
Далее имеем:
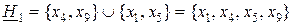 ;
;
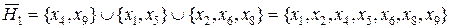 ; (4.36)
; (4.36)
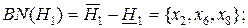
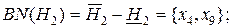
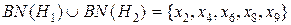 .
.
Включим, например, значение x2 в класс H1, а х9 - в Н2:
Hl = {xl, x2, x5};
H2 = {x3, x6, x7, x8, х9, x10};
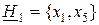 ;
;
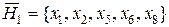 ;
;
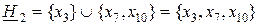 ; (4.37)
; (4.37)
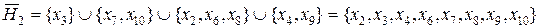 ;
;
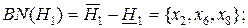
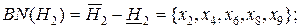
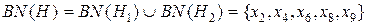 .
.
Выполненные проверки показали, что в обоих случаях граничная область не меняется и включает в себя элементы х2 и х9. Это подтверждает вывод, сделанный в [42]о том, что в случае, когда в начальном обучающем универсуме существует пример (примеры) с неизвестной принадлежностью к классу (классам), и этот пример (примеры) принадлежит граничной области классификаций, выполненных на основе всех других примеров, то влияние на результаты классификации исходного обучающего универсума не происходит.
Рассмотренные примеры указывают на возможность формирование набора решающих правил (классификатора), с помощью которого могут быть классифицированы новые примеры, которые не входили в состав исходного обучающего универсума. В основе такой классификации может быть положена следующая последовательность процедур [42]:
1. Для каждого нового примера и для каждого класса проверяется принадлежит ли данный пример нижней аппроксимации, отрицательной области или граничной области каждого конкретного класса.
2. Если пример принадлежит нижней аппроксимации конкретного класса, то он со 100%-ной уверенностью может быть идентифицирован как принадлежащий данному классу.
3. Если пример принадлежит отрицательной области конкретного класса, то он со 100% уверенностью может быть идентифицирован как принадлежащий данному классу.
4. Если же пример принадлежит граничной области конкретного класса, то нельзя сказать ничего определенного относительно принадлежности или непринадлежности этого примера к данному классу.
СПИСОК ЛИТЕРАТУРЫ
1. Айзерман М.А. Динамический подход к анализу структур, описываемых графами (основы графодинамики) I [Текст] / М.А. Айзерман, Л.А. Гусев, С.В. Петров, И.М. Смирнова // Автоматика и телемеханика. – 1977. – №7. – с.135–151.
2. Айзерман М.А. Динамический подход к анализу структур, описываемых графами (основы графодинамики) II [Текст] / М.А. Айзерман, Л.А. Гусев, С.В. Петров, И.М. Смирнова // Автоматика и телемеханика. – 1977. – №9. – с.123–136.
3. Акимова О.В. Методический подход к выбору типа судна для работы на заданном направлении перевозок [Текст] / О.В. Акимова, А. Г. Шибаев, В.Ю. Акимов// Сб. науч. трудов ОНМУ, 2012. – №19. – С. 124–139.
4. Андрейчиков А.В. Качественное моделирование рисковых ситуаций в экономике [Текст] /А.В. Андрейчиков // Вестник машиностроения, 2004. – №6. – С. 69–76.
5. Балякин О.К. Технология судоремонта [Текст] / О.К. Балякин, В.И. Седых, В.В. Тарасов. – М.: Транспорт, 1992. – 165 с.
6. Бень А.П. Использование метода анализа иерархий для принятия решений в сфере судоремонта [Текст] / А.П. Бень, О.В. Терещенкова//Вестник Херсонского национального университета, 2009. – №1(34). – С.434-437.
7. Бень А.П. Система поддержки принятия решений оперативного контроля судоремонта [Текст] / А.П. Бень//Вестник Херсонского национального университета, 2008. – №3(32). – С.49–53.
8. Блинов Э.К. Техническая эксплуатация флота и современные методы судоремонта [Текст] / Э.К. Блинов. – Л.: Судостроение, 1990. – 216 с.
9. Борисов А.Н. Вероятностный вывод в интеллектуальных система: Учебное пособие [Текст] / А.Н. Борисов, О.И. Ужта-Ребров, К.И. Савченко. – Рига, 2002. – 213 с.
10. Борисов А.Н. Принятие решений на основе нечетких моделей [Текст] / А.Н. Борисов, О.А. Крумберт, И.П. Федоров. – Рига: Зинатне, 1990. – 184 с.
11. Бугаенко Б.А. Расчетное определение оптимального варианта технологического процесса сварки судового набора на стапеле [Текст] / Б.А. Бугаенко, С.В. Драган, В.Я. Сагань // Проблемы техники. – 2009. – №1. – С.71–81.
12. Валькман Ю.Р. Моделирование НЕ-факторов – основа интеллектуализации компьютерных технологий [Текст] / Ю.Р. Валькман, В.С. Быков, А.Ю. Рыхальский // Системні дослідження та інформаційні технології, 2007. – №1. – С.39–61.
13. Винников В.В. Системы технологий на морском транспорте (перевозка и перегрузка грузов): Учебное пособие [Текст] / В.В. Винников, Е.Д. Быкова. – О.: Фенікс, 2006. – 186 с.
14. Горбачев С.А. Организационно-технологические пути снижения накладных расходов на постройку судов [Текст] / С.А. Горбачев, А.В. Догадин // Судостроение. – 1999. – №1. – С.44–46.
15. Драган С.В. Автоматизированный выбор оптимального технологического процесса сварки корпуса судна [Текст] / С.В. Драган, В.Я. Сагань // Зб. наук. праць НУК. – Миколаїв: НУК, 2007. - №4(415). – С. 38–45.
16. Заде Л. Лингвистическая переменная и теория нечетких множеств [Текст]/ Л.Заде. – М.: Мир, 1979. – 168 с.
17. Згуровский М.З. Системный анализ в исследовании сложных физических процессов и полей [Текст] / М.З. Згуровский, А.Н. Новиков, И.И. Коваленко и др. – К.: НК, 1993. – 37 с. – (Препр. Ин-та кибернетики им. В.М. Глушкова НАН Украины 1993).
18. Згуровский М.З. Системный анализ: проблемы, методология, приложения [Текст] /М.З Згуровский, Н.Д. Панкратова. – К.: Наукова думка, 2005. – 743 с.
19. Згуровский М.З. Технологическое предвидение [Текст] /М.З Згуровский, Н.Д. Панкратова. – К.: «Політехніка», 2005. – 156 с.
20. Здорнов В.А. Моделирование стоимости постройки в инвестиционных проектах кораблей [Текст] / В.А. Здорнов // Судостроение. –2005. – №5. – С. 60–61.
21. Исаев А.А. Обоснование стоимости постройки судов [Текст] / А.А. Исаев // Судостроение. – 2003. – №4. –С.36–39.
22. Коваленко И.И. Системный анализ задач судового корпусостроения: монография [Текст] / И.И. Коваленко, С.В. Драган, В.Я. Сагань. – Николаев: el Talisman, 2010. – 176 с.
23. Коваленко И.И. Экспертное ранжирование иерархических организационных структур с использованием метода анализа иерархий и теории свидетельств [Текст] / И.И. Коваленко, А.В. Швед, Е.С. Пугаченко // Вестник ХНТУ, 2013. – №1(46). – С. 67–71.
24. Коваленко И.И. Экспертные технологии поддержки принятия решений: монография [Текст] / И.И. Коваленко, А.В. Швед. – Николаев: Илион, 2013. – 216 с.
25. Ковтун Т.А. Применение методического подхода к инициализации проекта предоставления транспортной услуги / Т.А. Ковтун// Сб. науч. трудов ОНМУ, 2010. – №3. – С. 207-222.
26. Курлянд А.М. Метод оптимизации параметров судов, обеспечивающих океанско-фидерную систему доставки груза [Текст] / А.М. Курлянд, М.Я. Постан, И.В. Савельева // Сб. науч. трудов ОНМУ, 2010. – №15. – С. 7–17.
27. Організаційно-методичний документ: ОМД 22460848.003-2012. Крани портальні, крани-перевантажувачі. Експертне обстеження: проект. – Київ: [б.в.], 2012. – 136 с.
28. Нариньяни А.С. Неточность как Не-фактор. Попытка до формального анализа [Текст] / А.С. Нариньяни. - Москва-Новосибирск, 1994. – 34 с. – (Препринт /РосНИИ ИИ № 2 1994).
29. Панкратова Н.Д. Моделі і методи аналізу ієрархій. Теорія. Застосування [Текст] /Н. Д. Панкратова, Н.І. Недашківська. – К.: НТУУ «КПІ», 2010. – 372 с.
30. Румб В.К. Применение методики формализованной оценки безопасности для определения остаточного ресурса главного судового двигателя [Текст] / В.К. Румб, В.В. Медведев // Судостроение. – 2005. – №5. – С. 42–47.
31. Рылов С.И. Оценка Фрахтователем степени соответствия судна особенностям перевозки груза [Текст] /С.И. Рылов, Ю.А. Коскина // Сб. науч. трудов ОНМУ, 2009. – №2. – С. 94–103.
32. Рылов С.И. Фрахтование морских судов: учебное пособие [Текст] / С.И. Рылов, Я.А. Горшков. – Одесса: ОГМУ, 1999. – 174 с.
33. Саати Т. Аналитическое планирование. Организация систем [Текст] / Т. Саати, К. Кернс. – М.: «Радпо и связь», 1991. – 223 с.
34. Саати Т. Принятие решений при зависимостях и обратных связях [Текст] / Т. Саати. – М.: Изд-во ЛКИ, 2008. – 360 с.
35. Саати Т. Принятие решений. Метод анализа иерархий [Текст] / Т. Саати. – М.: «Радпо и связь», 1993. – 278 с.
36. Ужга-Ребров О. Особенности представления знаний в теории грубых множеств [Текст] / О. Ужга-Ребров // Матер. научно-практ. междунар. конфер. «Enviroment. Technology. Resourse. Proceeding» – Резекне, т.2. – С.169–175.
37. Юдицкий С.А. Разработка целевых сценариев для организационных систем [Текст] / С.А. Юдицкий, П.Н. Владиславлев // Приборы и системы управления. – 2002. – №12. – С.60–64.
38. Beynon M.J. DS/AHP method: A mathematical analysis, including an understanding of uncertainty [Text] / M.J. Beynon // European Journal of Operational Research. – 2002. – vol. 140. – P. 148–164.
39. Pawlak Z. Rough Sets Theoretical Aspects of Reasoning about Data [Text] / Z. Pawlak. – Boston; London: Academic Publishers, 1991. – 229 p.
40. Shafer G.A. A mathematical theory of evidence [Text] / G/ Shafen. – Princeton: Princeton University Press. – 1976. – 297 p.
41. Smarandache F. Advances and applications of DSmT for Information Fusion [Electronic resource] / F. Smarandache, J. Dezert // Rehoboth: American Research Press, 2006. – vol.2. – 461 p.
42. Uzga-Rebrovs O. Nenoteiktiby parvaldisana [Text] / O. Uzga-Rebrovs. – Rezekne: RA Izdevnieciba, 2010. – vol.3. – 560 lpp. – ISBN 978-9984-44-041-5.
Дата добавления: 2021-03-18; просмотров: 502;











