Принятие решений по выбору типов судов для перевозки грузов на основе нечетких отношений
Одной из задач при определении вариантов технологий морских грузоперевозок является выбор типа судов. При этом учитывается как структура перевозимых грузов, так и технические возможности судов, а также степень их универсальности [13].
Например, ролкеры могут перевозить более широкую номенклатуру грузов, чем контейнеровозы, лихтеровозы и т.д. Основным критерием для сравнения вариантов является уровень затрат на освоение всего грузопотока на рассматриваемом направлении. Эффективным считается тот вариант, который обеспечивает минимум затрат или максимум прибыли при определенном качестве перевозочного процесса (сохранность груза, скорость его доставки и др.).
Учитывая то, что отечественный торговый флот характеризуется малочисленностью, технической изношенностью, отсутствием новых прогрессивных типов судов, нужно отметить, что повышение эффективности перевозок может обеспечиваться учетом дополнительных факторов как количественного, так и качественного характера. Такая задача может решаться с использованием системного подхода и современных математических методов принятия решений.
С учетом сказанного, выбор технологии перевозок, и в частности, типа судна, может быть сведен к многокритериальному принятию решений посредством определения порядка (строгого или нестрогого) на множестве альтернатив, в качестве которых выступают различные типы судов.
Рассмотрим один из подходов к решению задачи выбора типов судов для перевозок грузов посредством формирования их ранжировок по степени предпочтения и оценивания таких ранжировок с использованием методов нечетких отношений.
В основу такого подхода может быть положена схема тяготения основных видов перевозимых морем грузов к типам судов, рассмотренная в работе [13] и представленная на рис. 4.2. Данная схема характеризуется следующими особенностями: с одной стороны, какой-либо вид грузов может перевозиться несколькими типами судов (например, для перевозки сухой нефти могут быть использованы танкеры и комбинированные суда), а с другой – одним типом судна могут быть перевезены различные виды грузов (например, балкерами).
Данное обстоятельство может создавать некоторые неопределенности в выборе типа судов (альтернативы) в зависимости от вида грузов (критерии). Для формирования ранжировок альтернатив достаточно широко применяется метод попарного сравнения, позволяющий получать совокупность бинарных отношений. Однако, исходя из вышесказанного, такие отношения могут обладать неточностью (нечеткостью). Следовательно, для принятия решения о выборе типа судна, можно воспользоваться основными положениями теории нечетких отношений.
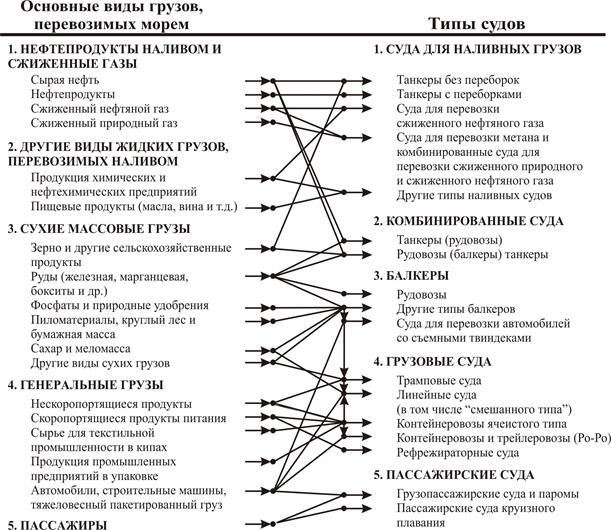
Рис. 4.2. Схема тяготения основных видов перевозимых морем грузов
к типам судов [13]
Рассмотрим задачу упорядочения многокритериальных альтернатив с применением нечетких бинарных отношений. Пусть задано множество m альтернативных решений X={x1,x2,…,xm} (типов судов), которое оценивается с помощью n критериев k1,k2,…,kn (виды грузов). Предполагается, что лицо, принимающее решение (ЛПР) или эксперт могут сравнить по предпочтительности все возможные пары решений (xi, xj) Î X.
Результаты такого сравнения по каждому и критериев могут быть отражены в форме нечетких бинарных отношений 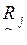 , j=1,..,n:
, j=1,..,n:
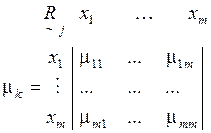 (4.10)
(4.10)
Чтобы решить задачу выбора рациональных решений, необходимо произвести сравнение альтернативных решений по всему множеству критериев. Такое сравнение в принципе может быть выполнено с использованием процедуры пересечения вида 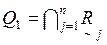 . В результате получается результирующее нечеткое бинарное отношение предпочтений
. В результате получается результирующее нечеткое бинарное отношение предпочтений 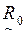 :
:
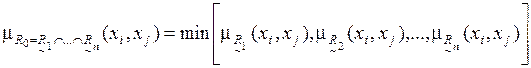 (4.11)
(4.11)
Если решается одна из типовых задач принятия решений, связанная с определением порядка (строгого или нестрогого) на множестве альтернатив, то полученное результирующее нечеткое бинарное отношение должно быть проверено на наличие рефлексивности, антисимметричности и транзитивности в соответствии со следующими условиями:
–  называется рефлексивным, если
называется рефлексивным, если
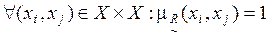 . (4.12)
. (4.12)
–  называется антисимметричным, если
называется антисимметричным, если
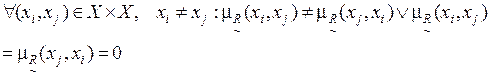 (4.13)
(4.13)
–  называется транзитивным, если
называется транзитивным, если
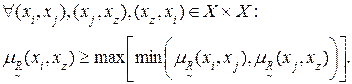 (4.14)
(4.14)
Проверка условий (4.12), (4.13) не составляет особого труда, так как при наличии рефлексивности на главной диагонали матрицы (4.10) стоят только единицы, а антисимметричность характеризуется неравенством значений функции принадлежности, симметрично расположенных относительно главной диагонали той же матрицы.
Проверку 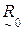 на транзитивность проведем по схеме, рассмотренной ранее. Прежде всего, необходимо задать
на транзитивность проведем по схеме, рассмотренной ранее. Прежде всего, необходимо задать 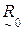 в виде таблицы, отображающей в числовом виде степени принадлежности пар (xi, xj) данному нечеткому бинарному отношению, и по этим значениям построить нечеткий граф. Далее, для каждой вершины графа необходимо сравнить значение функции принадлежности
в виде таблицы, отображающей в числовом виде степени принадлежности пар (xi, xj) данному нечеткому бинарному отношению, и по этим значениям построить нечеткий граф. Далее, для каждой вершины графа необходимо сравнить значение функции принадлежности 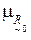 для дуги, выходящей из этой вершины и входящей в нее со значениями той же функции для каждого набора дуг, по которым можно выйти и снова достичь рассматриваемой вершины. Аналогично, значение
для дуги, выходящей из этой вершины и входящей в нее со значениями той же функции для каждого набора дуг, по которым можно выйти и снова достичь рассматриваемой вершины. Аналогично, значение 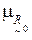 для каждой дуги, соединяющей две вершины, необходимо сравнить со значениями той же функции для всех возможных наборов дуг, соединяющих пару вершин нечеткого графа. Для этого используются различные композиции нечетких отношений по следующему максиминному правилу:
для каждой дуги, соединяющей две вершины, необходимо сравнить со значениями той же функции для всех возможных наборов дуг, соединяющих пару вершин нечеткого графа. Для этого используются различные композиции нечетких отношений по следующему максиминному правилу:
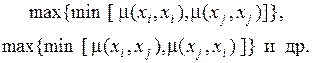 (4.15)
(4.15)
Выполнение всех трех условий (4.12), (4.13) и (4.14) позволяет утверждать, что на множестве упорядоченных пар нечетких бинарных отношений (xi, xj) должно существовать нечеткое отношение порядка, которое может быть получено посредством формирования определенного числа схем предпочтений (по числу рассматриваемых альтернативных решений) и проверкой их на транзитивность.
Приведем числовой пример. Пусть рассматривается m=3: X = {x1, x2, x3} альтернативных решений, которые необходимо оценить по n=3: K = {k1, k2, k3} критериям. ЛПР или эксперты выразили свои нечеткие предпочтения на данных альтернативах по каждому из критериев с различными значениями функции принадлежности μ Î [0,1] в виде следующих матриц:
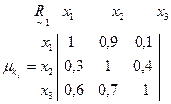
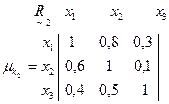
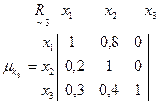
Выполним операцию 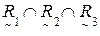 с учетом условия (4.11), в результате чего получим результирующее нечеткое бинарное отношение
с учетом условия (4.11), в результате чего получим результирующее нечеткое бинарное отношение 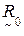 , для которого построим нечеткий граф (рис. 4.3):
, для которого построим нечеткий граф (рис. 4.3):
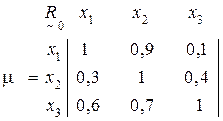
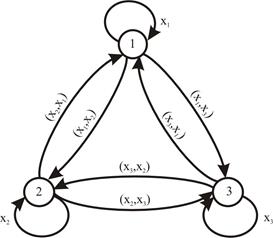
Рис.4.3. Нечеткий граф бинарного отношения 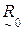
Проведем сравнение значений μ как для вершин графа, так и для возможных их пар.
1. Для вершины 1 имеем:
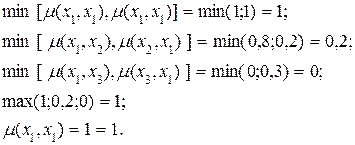
2. Для вершины 2 имеем:
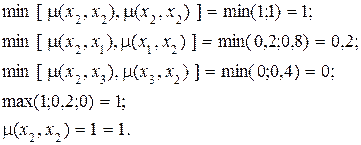
3. Для вершины 3 имеем:
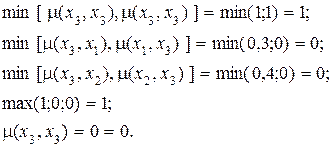
4. Для вершин 1 и 2 имеем:
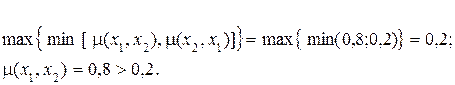
5. Для вершин 1 и 3 имеем:
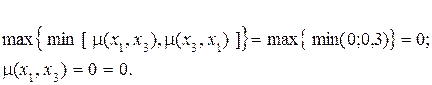
6. Для вершин 2 и 3 имеем:
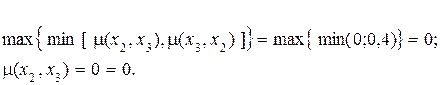
Таким образом, исследуемое результирующее нечеткое бинарное отношение 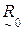 удовлетворяет всем трем условиям наличия в нем нечеткого отношения порядка.
удовлетворяет всем трем условиям наличия в нем нечеткого отношения порядка.
Выполним его поиск, предварительно сформировав 6 следующих возможных (при n=3) схем предпочтений:
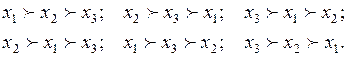 (4.16)
(4.16)
Проверим последовательно схемы (4.16) на транзитивность:
1. 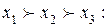 Если
Если 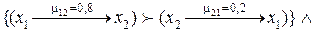
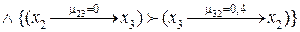 ,
то ,
то 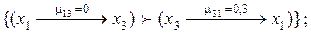 2.
2. 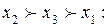 Если
Если 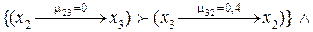
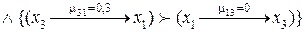 ,
то ,
то 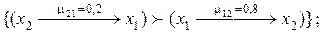 3.
3. 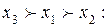 Если
Если 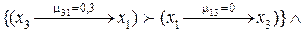
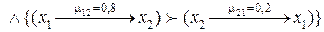 ,
то ,
то 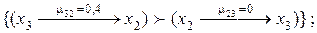 4.
4. 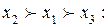 Если
Если 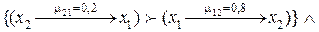
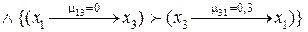 ,
то ,
то 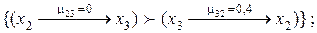 5.
5. 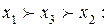 Если
Если 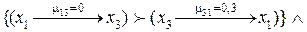
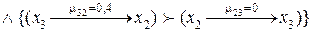 ,
то ,
то 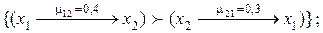 6.
6. 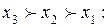 Если
Если 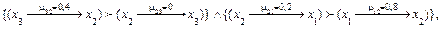 то
то 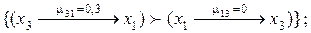
| (4.17) |
Третья схема предпочтений x3 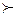 x1
x1 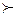 x2 является транзитивной, и следовательно альтернатива x3 – лучшей.
x2 является транзитивной, и следовательно альтернатива x3 – лучшей.
Рассмотренный подход для решения задачи выбора типов судна для перевозки грузов в условиях неопределенности, для анализа которых применен аппарат теории нечетких отношений, легко реализуется в вычислительном плане и может быть полезным для решения практических задач морских перевозок.
Дата добавления: 2021-03-18; просмотров: 528;











