Абстрактные автоматы. Методы описания и свойства
Значения дискретных функций переходов d и выходов l можно задавать таблицами. Иногда используют отдельные таблицы для каждой функции, но вместо пары таблиц удобнее взять одну объединенную таблицу с общими заголовками строк и столбцов. Для автомата Мили такая нестандартная таблица переходов и выходов выглядит как табл. 2.1.
Таблица 2.1
| х1 | х2 | |
| а0 | а1 / у1 | а2 / у2 |
| а1 | а3 / у2 | а0 / у1 |
| а2 | а2 / у2 | а3 / у3 |
| а3 | а1 / у1 | а1 / у2 |
Число столбцов в такой таблице равно числу букв абстрактного входного алфавита, а число строк - числу возможных состояний, т.е. числу букв внутреннего алфавита. Значения аргументов функций d и l указываются в заголовках строк и столбцов, а значения функций - в клетках таблицы.
Те же функции можно задать более наглядно с помощью ориентированного графа (рис. 2.1).
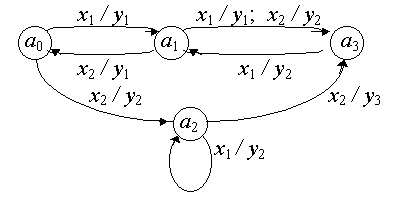
Рис. 2.1.
Состояния автомата изображаются вершинами графа, а переходы - дугами, около которых записываются соответствующие входные и выходные буквы. Кратные дуги заменяются одной дугой, около которой делаются записи, соответствующие всем переходам, определенным для данной пары состояний.
Функции d и l автомата Мура задаются так называемой "отмеченной" таблицей переходов (табл. 2.2), где каждому состоянию автомата присвоена "отметка" выходного сигнала.
Таблица 2.2
| х1 | х2 | |
| а0 / у1 | а1 | а2 |
| а1 / у2 | а3 | а0 |
| а2 / у1 | а2 | а3 |
| а3 / у2 | а1 | а1 |
Граф автомата Мура отличается от графа автомата Мили тем, что буквы выходного алфавита записываются не над дугами, а над вершинами (рис. 2.2).
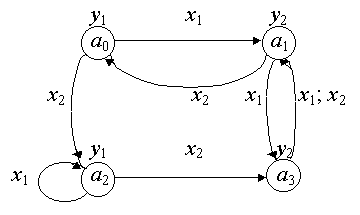
Рис. 2.2
Из приведенных примеров видно, что строение таблиц и графов определяется в основном функцией переходов, а функция выходов имеет подчиненное значение. Действительно, несмотря на то, что работа автомата состоит в формировании выходных слов, не функция выходов, а именно функция переходов является главной в определении свойств автомата. С этой функцией бывают связаны и основные проблемы синтеза автоматов.
В тех случаях, когда функция переходов рассматривается самостоятельно, вне связи с функцией выходов, применяется ещё один способ её задания. Это - матрица входов или "квадратная автоматная матрица". Её горизонтальными входами служат старые состояния а(t), а вертикальными - новые состояния а(t+1). Стало быть, матрица читается "от строки к столбцу". На пересечении строк и столбцов, т.е. в клетках матрицы записываются входные буквы, вызывающие данный переход. Если данная пара состояний не связана переходом, в клетке матрицы делается прочерк, а если переход определен при нескольких буквах "х", все эти буквы записываются через запятую.
Для обоих представленных выше автоматов матрица входов одинакова:
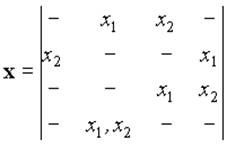
Перейдем к определению основных свойств, которыми могут обладать абстрактные автоматы.
Практический интерес представляют только детерминированные автоматы, у которых функции d и l являются функциями в строгом смысле этого слова, т.е. определяются однозначно. В теории допускается существование недетерминированных автоматов, которые обладают возможностью совершая очередной переход в новое состояние выбирать его из некоторого подмножества алфавита А.
Все состояния автомата должны быть достижимыми, т.е. должна существовать возможность перевода автомата в любое из состояний за конечное число переходов. Так как работа автомата всегда начинается из состояния а0, на графе автомата должны существовать пути от начальной вершины ко всем остальным. Другими словами, граф автомата должен быть связным.
Автомат обладает полной системой переходов, если любые два состояния связаны парой переходов встречного направления, а также возможно сохранение любого из состояний. На графе такого автомата все вершины попарно соединены дугами встречного направления и у каждой вершины есть петля (рис. 2.3). Такие автоматы, очевидно, обладают универсальными возможностями для реализации алгоритмов, так как могут быть переведены в любое из своих состояний за один интервал автоматного времени.
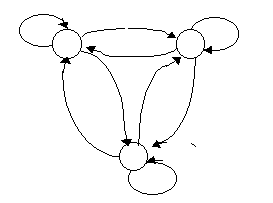
Рис. 2.3
На рис. 2.4 показан граф детерминированного автомата со всеми достижимыми состояниями, не обладающего полнотой системы переходов.
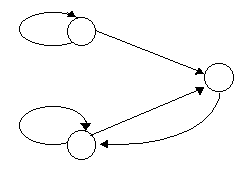
Рис. 2.4
У автомата с полной системой переходов в таблице переходов каждая строка должна содержать все буквы внутреннего алфавита, а в матрице входов не должно быть прочерков.
Автомат Мили обладает полной системой выходов, если для каждой пары (а, х) функция выходов имеет разные значения. При этом число букв в выходном алфавите оказывается равным произведению мощностей внутреннего и входного алфавитов |Y| = |A|*|X|.
У автомата Мура полная система выходов получается при совпадении числа букв в алфавитах A и Y. В этом случае нет необходимости давать разные обозначения буквам внутреннего и выходного алфавитов, так как один из этих алфавитов (обычно внутренний) достаточен для описания работы автомата.
Частичными автоматами называются ЦА, у которых функции d и l определены не для всех пар (а, х). Пары значений аргументов, соответствующие неопределенным значениям функций, т.е. не принадлежащие области определения этих функций, называются запрещенными парами по аналогии с запрещенными наборами значений аргументов частичных функций алгебры логики.
В таблице переходов частичного автомата в некоторых клетках имеются прочерки (табл. 2.3).
Таблица 2.3
| x1 | x2 | x3 | x4 | x5 | |
| a0 | a1 | - | a0 | a1 | a2 |
| a1 | a1 | a0 | a6 | a2 | a0 |
| ... | ... | ... | ... | ... | ... |
Согласно таблицы 2.3 функция переходов не определена на паре (а0, х2), т.е. автомат не должен каким-то определенным образом реагировать на слова, начинающиеся с буквы х2.
Дата добавления: 2020-06-09; просмотров: 1011;











