Основы теории грубых множеств (ТГМ)

Рассмотрим основные положения теории грубых множеств согласно их изложению в работах [36, 39, 42].

Теория грубых множеств (ТГМ) рассматривается, как концепция и теоретическая основа рассуждения о знаниях, когда они не точны (неупорядоченные знания). Данная теория основана на том, что знания глубоко внедрены в способность людей выполнять классификацию предметов, явлений, объектов, ситуаций и др. Другими словами, знания основаны на способности классифицировать объекты. Поэтому знания в ТГМ обязательно связаны с множеством образцов классификации, относящихся к специфическим частям реального или абстрактного мира, называемого универсумом рассуждений (или, кратко, универсумом).

Фактически знания состоят из семейства различных образцов классификации интересующей предметной области.

Пусть U ≠ Æ конечное множество (универсум), рассматриваемых объектов. Любое подмножество X Í U универсума (Í – нестрогое включение, т.е. допускается, что X = U) называется категориейв U и любое семейство категорий в U считается знаниями.

ТГМ основана на категориях, которые формируют разбиение (классификацию) определенного универсума U, то есть на получении семейства С = {Х₁,Х₂,...,Х_п}, такого что X_i Í U, X_i≠Æ, X_i Ç X_j=Æ для і≠j, (i,j =1,…,n) и È X_i = U. Такое семейство называется базой знаний на U, которая представляет множество основных аспектов классификации (цвет, температура и т.д.).

В ТГМ предлагается процедуры классификации выполнять с использованием отношений эквивалентности. Тогда под базой знаний понимают реляционную систему K=(U,R), где U≠Æ конечное множество, называемое универсумом и R - семейство отношений эквивалентности. Если R - отношение эквивалентности на U, тогда через U/R обозначается семейство всех классов эквивалентности R, которые называют категориями, через [x]_R обозначают категорию в R, содержащую элемент xÎU.

Если PÍR и P≠Æ тогда ÇР (пересечение всех отношений эквивалентности, принадлежащих Р) также является отношением эквивалентности, обозначаемым через IND(P) и называется отношением неразличимости.

Более того, 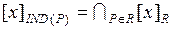. Поэтому U/ IND(P) (то есть, семейство всех классов эквивалентности IND(P)) обозначает знания, связанные с семейством эквивалентности Р, которые называются Р-основными знаниями относительно U в K. Для простоты в дальнейшем вместо U/IND(P) будет писаться U/P. Классы эквивалентности IND(P) называются основными категориями. В частности, если QÎR, то Q называется Q-элементарными знаниями относительно U в K, и классы эквивалентности Q называются Q-элементарными категориями знаний R.

Например, если элементы универсума разделяются на категории „цвет", то элементарными категориями будут подмножества всех объектов, имеющих специфические цвета: „зеленый", „красный" и т.д., в то время, как основными категориями являются комбинации некоторых элементарных категорий. Например, если „старый" и „больной" являются элементарными категориями, то „старый и больной" является основной категорией в этой базе знаний.

Фактически Р-основные категории являются такими основными свойствами универсума U, которые могут быть выражены, используя знания Р. Другими словами, они являются фундаментальными строительными блоками наших знаний или основными свойствами универсума.

Семейство всех Р-основных категорий для всех Æ≠РÍR называется семейством основных категорий в базе знаний K=(U,R).

Вводится также следующее обозначение: пусть K=(U,R) – база знаний. Через IND(K) обозначается семейство всех отношений эквивалентности, определенных на К как

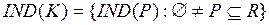(4.18)

Каждое объединение Р-основных категорий называется Р-категорией. Окончательно, семейство всех категорий в базе знаний K=(U,R) будет относиться к K-категориям.

Классы эквивалентности элементов (объектов) на универсуме выделяются на основе признаков. Если признаком элемента, например, является его „цвет", то могут быть выделены подмножества (элементарные категории) элементов, обладающих различными оттенками одного и того же цвета. Важно подчеркнуть, возможные небольшие отличия в значениях релевантного признака игнорируются в пределах элементарной категории. Так, если в одну категорию включены элементы, обладающие различными оттенками красного цвета, то эти оттенки игнорируются и все такие элементы считаются красными элементами.

Если значения релевантного признака являются непрерывной величиной, то для определения элементарных категорий должны быть выделены соответствующие интервалы значений признака. Например, возраст может быть разбит на три интервала: „молодой", „средний" и „старый". Тогда отнесение индивида к одному из них будет жестко связано с границами таких интервалов. Так, если граница между категориями „средний" и „старый" будет равна 60 лет, то индивид в возрасте 59 лет будет отнесен к категории людей среднего возраста, а индивид в возрасте 61 год будет отнесен к категории старых людей. Этим идеология грубых множеств полностью отличается от идеологии нечетких множеств. При использовании второго подхода индивид в возрасте 59 лет может одновременно принадлежать к множеству среднего возраста и к множеству старого возраста с различными значениями принадлежности, а все элементы любой категории в теории грубых множеств считаются неразличимыми.

Если производится классификация элементов универсума по значениям различных признаков, то результатами такой классификации будут основные категории, каждая из которых является пересечением, а также возможно и объединением соответствующих элементарных категорий.

Рассмотрим еще один принцип ТГМ. Пусть K=(U,Р) и K¢ =(U,Q) – две базы знаний. Если при этом IND(P) Ì IND(Q), то говорят, что Р (база знаний K) точнее, чем знания Q (база знаний K¢), или наоборот Q грубее, чем Р. Тогда считается, что если Р точнее, чем Q, то Р является специализацией Q, а Q является обобщением Р.

Пример. Пусть Р, Q Î R и U/P, и U/Q являются классификациями универсума „цвет". U/P – содержит одну классификацию, скажем, зеленых объектов, a U/Q – содержит больше категорий зеленых объектов, каждая из которых учитывает специфические оттенки зеленого цвета.

Тогда Q является специализацией Р, и Р является обобщением Q, обеспечивая при этом включение всех категорий оттенков зеленого в U / P, т.е. U/Q Ì U /Р.

Поэтому обобщение состоит в комбинации некоторых категорий, в то время, как специализация состоит в разделении категорий на более точные единицы.

Необходимо упомянуть, что если все классы отношения эквивалентности являются множествами единственных (единичных) элементов, то тогда отношение является отношением равенства. В таком случае отношение представляет наиболее точные знания. Однако такая ситуация бывает не часто.

Возвратимся к примеру с цветами. Точное различение цветов не позволяет сформулировать одну категорию, скажем, зеленого цвета. Поэтому, чтобы иметь категорию такие, как „зеленый", „красный", „низкий", „высокий „горячий", „холодный" и так далее, необходимо иметь возможность комбинировать объекты в группы, игнорируя „малые" различия между ними или, другими словами группировать их вместе соответственно с их подобием. То есть в ТГМ используется своего рода „неточная" классификация, что на практике может выглядеть более реально, чем точная классификация для которой достаточно часто невозможно установить классификационную категорию.

Пусть K=(U,Р) – база знаний, где U – универсум элементов, R-отношение эквивалентности. Целевое множество XÍU называется R-определимым, если оно является объединением категорий, выделенных на универсуме посредством отношения эквивалентности R. В противном случае целевое множество X является R-неопределимым.

Иными словами, R-определимые множества – это те множества универсума, которые могут быть точно определены в базе знаний K, a R-неопределимые множества – это те подмножества универсума, которые не могут быть точно определены в этой базе знаний.

R-определимые множества называются также R-точными, a R- неопределимые множества называются R-неточными или R-грубыми.

Множество XÍU называется точным в базе знаний K, если существует отношение эквивалентности R Î IND(K), такое, что X R-точно. Целевое множество XÍU называется грубым, если X R-грубо для любого R Î IND(K).

Теория грубых множеств разработана для обращения с множествами, которые являются грубыми, в определенном выше смысле. Каким образом может быть представлено грубое множество, если оно не может быть представлено как точное объединение некоторых основных категорий универсума?

Теория грубых множеств предлагает специфическое аппроксимированное представление таких проблемных множеств.

Вводятся следующие определения. С каждым целевым множеством XÍU и отношением эквивалентности RÎIND(K) могут быть связаны два подмножества:

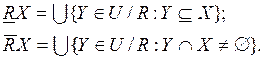(4.19)

которые называются R-нижней и R-верхней аппроксимацией целевого множества X, соответственно.

Используя ранее введенные обозначения данные выражения могут быть представлены в следующих альтернативных формах:

(4.20)

или 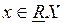, если и только если [x]_R Í X; 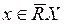, если и только если [x]_R Ç X≠Æ.

Согласно определению множество 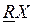является подмножеством элементов U, которые с определенностью могут классифицироваться как принадлежащие целевому множеству X; множество 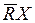это подмножество элементов U, которые возможно могут классифицироваться как принадлежащие целевому множеству X.

Вводятся дополнительные обозначения:

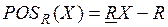– положительная область целевого множества X;

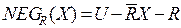– отрицательная область целевого множества X;

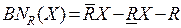–граничная область целевого множества X.

R-положительная область целевого множества X совпадает с R-нижней аппроксимацией этого множества и включает в себя все элементы, с определенностью принадлежащие X.

R-отрицательная область целевого множества X включает все те элементы универсума U, которые не принадлежат R-верхней аппроксимации этого множества.

По определению все элементы отрицательной области с определенностью не принадлежат целевому множеству X.

R-граничная область целевого множества X определяется как разность R-верхней и R-нижней аппроксимаций этого множества. Поэтому эта область включает элементы универсума, которые потенциально могут принадлежать множеству X. Это область неопределенности, для корректного обращения с которой и была разработана теория грубых множеств.

Элемент х целевого множества X называется R-положительным, если x Î POS_R(X).

Элемент х целевого множества X называется R-отрицательным элементом, если х Î NEG_r(X).

Элемент x целевого множества X называется R-граничным элементом, если х Î BN_r(X).

Имеют силу следующие очевидные свойства:

– целевое множество XR-определимо при существующих знаниях R, если и только если .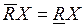

– целевое множество X грубо при существующих знаниях R, если .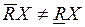

В общем случае R-нижняя и R-верхняя аппроксимации обладают рядом свойств, из которых наиболее важными являются следующие:

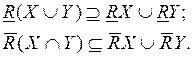(4.21)

Вводится понятие отношения принадлежности элемента универсума U определенному целевому, множеству. Это понятие основывается на концепции аппроксимации грубого множества двумя обычными множествами.

Поэтому в ТГМ вводятся два отношения принадлежности:

1. 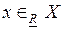, eсли и только если 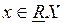. Это означает, что «элемент х определенно принадлежит целевому множеству X при существующих значениях R». Данное отношение называют нижним отношением принадлежности.

2. 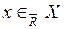, если и только если 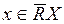. Это трактуется, что «возможно, что элемент х принадлежит целевому множеству X при существующих значениях R».

Такое отношение называют верхним отношением принадлежности.

В теории обычных множеств, принадлежность элемента множеству трактуется однозначно: элемент либо принадлежит данному множеству, либо нет. В теории грубых множеств понятие принадлежности элемента целевому множеству определяется более сложным образом: элемент может принадлежать либо нижней R-аппроксимации данного множества, либо его верхней аппроксимации, либо вообще не принадлежать данному множеству (в этом случае элемент принадлежит отрицательной области целевого множества). Принадлежность элемента нижней R-аппроксимации данного целевого множества X автоматически заключает, что этот элемент принадлежит верхней R-аппроксимации X. Однако, обратное верно не всегда, поскольку верхняя аппроксимация включает в себя и R-граничную область X.

Поскольку грубое множество моделирует неопределенность относительно принадлежности некоторых элементов универсума данному целевому множеству, представляется необходимым каким-то образом оценить степень этой неопределенности. Поэтому была введена следующая оценка точности аппроксимации:

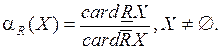(4.22)

Данная оценка отражает степень полноты существующих знаний и располагается в интервале a_r(X) Î[0,1].

Если R-граничная область множества X пуста, то есть 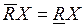, то a_R(X)= 1 и множество Х R-определимо.

Если R-граничная область Х не пуста, то a_R(X) < 1. Такие значения a_R(X) характеризуют R-неопределяемые или грубые множества.

Альтернативно данной оценке была ведена оценка грубости целевого множества X:

(4.23)

Данная оценка характеризует степень неполноты существующих знаний.

Наряду с данными оценками были введены более детальные классификации грубых множеств:

1. Есл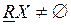и и 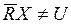, то Х грубо R-определимо.

Если X грубо R-определимо для некоторых элементов универсума U, то возможно определить принадлежат ли они области X или области - X универсума (положительной или отрицательной области целевого множества X).

2. Есл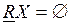и и 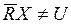, то X внутренне R-неопределимо.

Если X внутренне R-неопределимо, то для некоторых элементов универсума U возможно определить, принадлежат ли они области -X, но невозможно определить ни один элемент области X.

3. Есл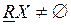и и 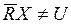, то X внешне R-неопределимо.

Если X внешне R-неопределимо, то для некоторых элементов универсума U возможно определить, принадлежат ли они области X, но невозможно определить ни один элемент -X.

4. Есл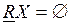и и 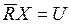, то Х тотально R-неопределимо.

Если X тотально R-неопределимо, то ни для одного элемента универсума U невозможно определить, принадлежит ли он области X или области - X.

Преимуществом рассмотренной классификации грубых множеств является то, что она отражает специфичность неопределенности внутренних структур таких множеств.

Рассмотрим пример формирования базы знаний, элементы которой представлены экспертными оценками на основе положений ТГМ [42]. Пусть экспертная группа задана в виде универсума U, состоящего, например из n=10 элементов (экспертов) 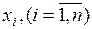, т.е. U = {x₁, x₂, х₃ ,...,x₁₀}. Каждому эксперту необходимо оценить 3 признака некоторого объекта (характеристики или показатели): а₁, а₂, а₃ по вербальной шкале со следующими градациями: 0 – «отлично»; 1 – «хорошо»; 2 – «плохо». Полученные таким образом экспертные оценки представлены в виде таблицы 4.19.

Таблица 4.19